如图,欲将一块四方形的耕地中间的一条折路MPN改直,但不能影响道路两边的耕地面积,应如何画线?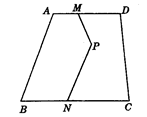
如图,反比例函数y= (x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=
(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB= .
.
(1)求k的值;
(2)将线段AB沿x轴正方向平移到线段DC的位置,反比例函数y= (x>0)的图象恰好经过DC上一点E,且DE:EC=2:1,求直线AE的函数表达式;
(x>0)的图象恰好经过DC上一点E,且DE:EC=2:1,求直线AE的函数表达式;
(3)若直线AE与x轴交于点,N,与y轴交于点M,请你探索线段AM与线段NE的大小关系,写出你的结论并说明理由.
我县某中学艺术节期间,向全校学生征集书画作品.九年级美术王老师从全年级14个班中随机抽取了A、B、C、D四个班,对征集到的作品的数量进行了分析统计,制作了如下两幅不完整的统计图.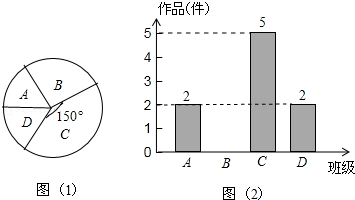
(1)王老师所调查的4个班共征集到作品多少件?请把图2补充完整;
(2)如果全年级参展作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生.现在要在其中抽两人去参加学校总结表彰座谈会,求恰好抽中一男一女的概率.(要求写出用树状图或列表分析过程)
某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:(注:利润=售价-进价)
| 甲 |
乙 |
|
| 进价(元/件) |
15 |
35 |
| 售价(元/件) |
20 |
45 |
若商店计划销售完这批商品后能使利润达到1100元,问甲、乙两种商品应分别购进多少件?
(1)如图,正方形AEFG的顶点E、G在正方形ABCD的边AB、AD上,连接BF、DF.求证:BF=DF;
(2)如图,在▱ABCD中,AD=4,AB=8,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,求阴影部分的面积.(结果保留π)
化简:
(1)
(2)解不等式组 ;并求它的最小整数解.
;并求它的最小整数解.