如图,墙壁上的展品最高点与地面的距离PF=3.2 m,最低点与地面的距离QF ="2" m,观赏者的眼睛E 距地面1.6 m.经验表明,当水平视线EH 与过P、Q、E 三点的圆相切于点E 时,视角最大,站在此处观赏最理想.求此时点E 到墙壁的距离EH.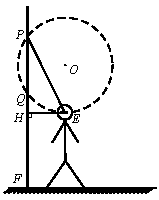

如图,点C、D 分别在∠AOB 的两边上.求作⊙P,使它与OA、OB、CD 都相切(不写作法,保留作图痕迹).
如图,AB 是半圆O 的直径,AD 和BC 是它的两条切线,切点分别为A、B,CO 平分∠BCD.
(1)求证:CD是半圆O的切线;
(2)若AC=2,BD=3,求AB的长..
某中学举行“校园好声音”歌手大赛,初、高中部根据初赛成绩,各选出5 名选手组成初中代表队和高中代表队参加学校决赛.每个队5 名选手的决赛成绩如图所示:
(1)填表:
(2)结合两队决赛成绩的平均数和中位数,分析哪个代表队的成绩较好;
(3)计算两队决赛成绩的方差,并判断哪个代表队的成绩较为稳定.
某旅行社为吸引市民组团去千岛湖旅游,推出如下收费标准:
某单位组织员工去千岛湖旅游,共支付给该旅行社旅游费用27000 元,请问该单位这次共有多少员工去旅游?