甲盒中有红、黑、白三种颜色的球各3个,乙盒中有黄、黑、白 三种颜色球各2个,从两个盒子中各取1个球
⑴求取出的两个球是不同颜色球的概率
⑵请设计一个随机模拟的方法来模拟⑴中的问题
已知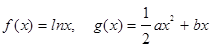

(1)当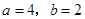 时,求
时,求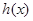 的极大值点;
的极大值点;
(2)设函数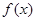 的图象
的图象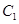 与函数
与函数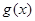 的图象
的图象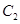 交于
交于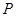 、
、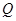 两点,过线段
两点,过线段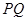 的中点做
的中点做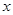 轴的垂线分别交
轴的垂线分别交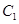 、
、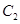 于点
于点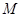 、
、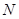 ,证明:
,证明: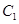 在点
在点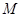 处的切线与
处的切线与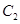 在点
在点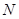 处的切线不平行.
处的切线不平行.
已知椭圆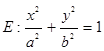 (a>b>0)的离心率为
(a>b>0)的离心率为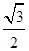 ,且过点(
,且过点(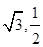 ).
).
(1)求椭圆E的方程;
(2)设直线l:y=kx+t与圆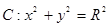 (1<R<2)相切于点A,且l与椭圆E只有一个公共点B.
(1<R<2)相切于点A,且l与椭圆E只有一个公共点B.
①求证: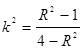 ;
;
②当R为何值时,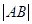 取得最大值?并求出最大值.
取得最大值?并求出最大值.
学生的数学学习水平按成绩可分成8个等级,等级系数X依次为1,2, ,8,其中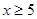 为标准A,
为标准A,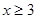 为标准B.已知甲学校执行标准A考评学生,学生平均用于数学的学习时间为3.5小时/天;乙学校执行标准B考评学生,学生平均用于数学的学习时间为2.5小时/天.假定甲、乙两学校都符合相应的执行标准.
为标准B.已知甲学校执行标准A考评学生,学生平均用于数学的学习时间为3.5小时/天;乙学校执行标准B考评学生,学生平均用于数学的学习时间为2.5小时/天.假定甲、乙两学校都符合相应的执行标准.
(1)已知甲学校学生的数学学习水平的等级系数X1的概率分布列如下所示:
| X1 |
5 |
6 |
7 |
8 |
| P |
0.4 |
a |
b |
0.1 |
且X1的数学期望EX1=6,求a、b的值;
(2)为分析乙学校学生的数学学习水平的等级系数X2,从该校随机选取了30名学生,相应的等级系数组成一个样本,数据如下:
3533855634
6347534853
8343447567
用这个样本的频率分布估计总体分布,将频率视为概率,求等级系数X2的数学期望;
(3)在(1)、(2)的条件下,哪个学校的数学学习效率更高?说明理由.
(注: )
)
平行四边形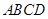 中,
中,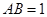 ,
,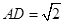 ,且
,且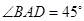 ,以BD为折线,把△ABD折起,
,以BD为折线,把△ABD折起,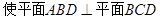 ,连接AC.
,连接AC.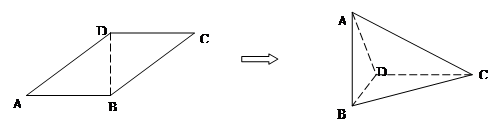
(1)求证:;
(2)求二面角B-AC-D的大小.
设△ABC的内角A、B、C所对的边长分别为a、b、c,且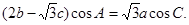
(1)求角A的大小;
(2)若角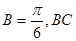 边上的中线AM的长为
边上的中线AM的长为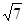 ,求△ABC的面积.
,求△ABC的面积.