(本小题12分)下表提供了工厂技术改造后某种型号设备的使用年限 和所支出的维修费用
和所支出的维修费用 (万元)的几组对照数据:
(万元)的几组对照数据:
 (年) (年) |
 |
 |
 |
 |
 (万元) (万元) |
 |
 |
 |
 |
(1)若知道 对
对 呈线性相关关系,请根据上表提供的数据,用最小二乘法求出
呈线性相关关系,请根据上表提供的数据,用最小二乘法求出 关于
关于 的线性回归方程
的线性回归方程 ;
;
(2)已知工厂技改前该型号设备使用10年的维修费用为9万元.试根据(1)求出的线性回归方程,预测该型号设备技改后使用10年的维修费用比技改前降低多少?
(本小题满分12分)如图,棱锥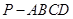 中,
中,  底面
底面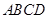 ,底面
,底面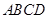 是矩形,
是矩形, ,
, .
.
(1)求证:平面 ⊥平面
⊥平面 ;
;
(2)在 边上是否存在一点
边上是否存在一点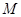 ,使得
,使得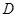 点到平面
点到平面 的距离为2,若存在,求
的距离为2,若存在,求 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
(本小题满分12分)某工厂生产 两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
 |
7 |
7 |
7.5 |
9 |
9.5 |
 |
6 |
 |
8.5 |
8.5 |
 |
由于表格被污损,数据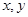 看不清,统计员只记得
看不清,统计员只记得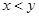 ,且
,且 两种元件的检测数据的平均值相等,方差也相等.
两种元件的检测数据的平均值相等,方差也相等.
(1)求表格中 与
与 的值;
的值;
(2)若从被检测的5件B种元件中任取2件,求2件都为正品的概率.
(本小题满分12分)在三角形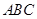 中,
中,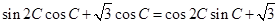 .
.
(1)求角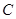 的大小;
的大小;
(2)若 ,且
,且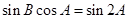 ,求
,求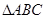 的面积.
的面积.
(本小题满分10分)已知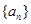 为等比数列,其中
为等比数列,其中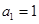 ,且
,且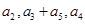 成等差数列.
成等差数列.
(1)求数列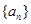 的通项公式;
的通项公式;
(2)设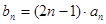 ,求数列
,求数列 的前
的前 项和
项和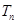 .
.
(本小题14分)设函数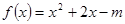 ,
,
(1)当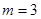 时,求函数f(x)的零点;
时,求函数f(x)的零点;
(2)当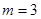 时,判断
时,判断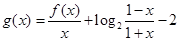 的奇偶性并给予证明;
的奇偶性并给予证明;
(3)当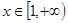 时,
时,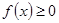 恒成立,求
恒成立,求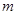 的最大值.
的最大值.