先阅读理解下面的例题，再按要求解答下列问题：
例题：求代数式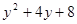
的最小值.
解：
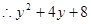的最小值是
.
（1）求代数式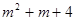
的最小值；
（2）求代数式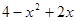
的最大值；
（3）某居民小区要在一块一边靠墙（墙长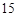
m）的空地上建一个长方形花园
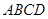，花园一边靠墙，另三边用总长为
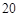m的栅栏围成. 如图，设
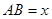（m），请问:当
取何值时，花园的面积最大？最大面积是多少？
已知：如图，
、
、
、
四点在一直线上，AF=CD，AB∥DE，且AB=DE，求证：△ABC≌△DEF．
已知，如图AB=AC，BD=CD，DE⊥AB于点E，DF⊥AC于点F，求证：DE=DF．
如图， AC与BD交于点E，且AC=DB，AB=DC．求证：∠A=∠D；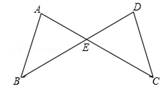
如图，已知直线l的函数表达式为
，且l与x轴、y轴分别交于A、B两点，动点Q从B点开始在线段BA上以每秒2个单位的速度向点A移动，同时动点P从A点开始在线段AO上以每秒1个单位的速度向O点移动，设点Q、P移动时间为t秒。
（1）求点A、B的坐标。
（2）当t为何值时，以点A、P、Q为顶点的三角形与△AOB相似？
如图所示，梯形ABCD中，AD∥BC，点E是边AD的中点，连接BE交AC于点F，BE的延长线交CD的延长线于点G。
（1）求证：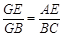
；
（2）若GE=2，BF=3，求线段EF的长。