如图,已知在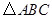 中,
中,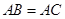 ,
,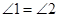 .
.
求证: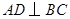 ,
,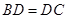 .
.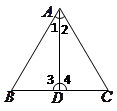
如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
(1)画出△ABC的AB边上的中线CD;
(2)画出△ABC向右平移4个单位后得到的△A1B1C1;
(3)图中AC与A1C1的关系是:_____________.
(4)图中△ABC的面积是_______________.
因式分解(1) 4a(x-y)-2b(y-x); (2) (3)
(3)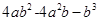
计算(1) 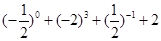 (2)
(2)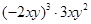
 (3)(x+1)2﹣(x+2)(x-2)
(3)(x+1)2﹣(x+2)(x-2)
某工厂用如图甲所示的长方形和正方形纸板做成如图乙所示的A,B两种长方体形状的无盖纸盒.现有正方形纸板140张,长方形纸板360张,刚好全部用完,问能做成多少个A型盒子?多少个B型盒子?
(1)根据题意,甲和乙两同学分别列出的方程组如下:
甲: 乙:
乙: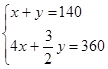
根据两位同学所列的方程组,请你分别指出未知数x,y表示的意义:
甲:x表示_________,y表示_________;
乙:x表示_________,y表示_________;
(2)求出做成的A型盒子和B型盒子分别有多少个(写出完整的解答过程)? 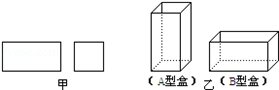
如图,∠1=∠ABC,∠2=∠3,FG⊥AC于F,判断BE与AC有怎样的位置关系,并说明理由。