已知抛物线 与
与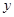 轴交于
轴交于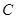 点,与
点,与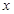 轴交于
轴交于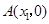 ,
,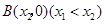 两点,顶点
两点,顶点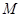 的纵坐标为
的纵坐标为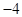 ,若
,若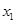 ,
,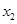 是方程
是方程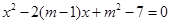 的两根,且
的两根,且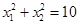 .
.
(1)求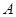 ,
, 两点坐标;
两点坐标;
(2)求抛物线表达式及点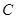 坐标;
坐标;
(3)在抛物线上是否存在着点 ,使△
,使△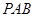 面积等于四边形
面积等于四边形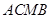 面积的2倍,若存在,求出
面积的2倍,若存在,求出 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
为了加强视力保护意识,小明想在长为3.2米,宽为4.3米的书房里挂一张测试距离为5米的视力表.在一次课题学习课上,小明向全班同学征集“解决空间过小,如何放置视力表问题”的方案,其中甲、乙、丙三位同学设计方案新颖,构思巧妙.
(1)甲生的方案:如下页图1,将视力表挂在墙ABEF和墙ADGF的夹角处(不考虑视力表与墙角AF之间的距离),被测试人站立在对角线AC上,问:甲生的设计方案是否可行?请说明理由.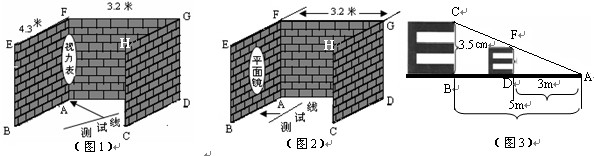
(2)乙生的方案:如图2,将视力表挂在墙CDGH上,在墙ABEF上挂一面足够大的平面镜,根据平面镜成像原理可计算得到:测试线应画在距离墙ABEF米处.
(3)丙生的方案:如图3,根据测试距离为5m的大视力表制作一个测试距 为3m的小视力表.如果大视力表中“E”的长是3.5cm,那么小视力表中相应“E”的长是多少cm?
下面是某同学对多项式(x2—4x+2)(x2—4x+6)+4进行分解因式的过程。
解:设x2—4x=y.
原式=(y+2)(y+6)+4(第一步)
=y2+8y+16(第二步)
=(y+4)2(第三步)
=(x2—4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了分解因式的;
A.提取公因式 B.逆用平方差公式 C.逆用完全平方公式
(2)该同学分解因式的结果不正确,应更正为;
(3)试分解因式n(n+1)(n+2)(n+3)+1.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B。
(1)求证:△ADF∽△DEC;
(2)若AB=4,AD=3 ,AE=3,求AF的长。
,AE=3,求AF的长。
“勤劳”是中华民族的传统美德,学校要求同学们在家里帮助父母做些力所能及的家务. 王刚同学在开学初针对暑假在家做家务的时间进行了抽样调查(时间取整数小时),所得数据统计如下表:
| 时间分组(时) |
0.5~20.5 |
20.5~40.5 |
40.5~60.5 |
60.5~80.5 |
80.5~100.5 |
| 频数(人) |
20 |
25 |
30 |
15 |
10 |
(1)在这个问题中的样本是,其中暑假做家务的时间在20.5~40.5的频率为_____.
(2)根据表中数据补全图中的频数分布直方图.
(3)样本的中位数所在时间段的范围是.
(4)若该学校有学生1260人,那么约有名学生在暑假做家务的时间在40.5~100.5小时之间。
如图所示,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.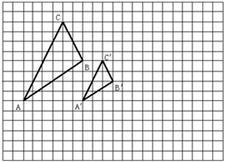
(1)画出位似中心点O;
(2)直接写出△ABC与△A’B’C’的位似比;
(3)以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,画出△A′B′C′关于点O中心对称的△A"B"C",如果△ABC内部一点M的坐标为(x,y),写出△A"B"C"中M的对应点M"的坐标。