某通讯器材公司销售一种市场需求较大的新型通讯产品．已知每件产品的进价为40元，每年销售该种产品的总开支（不含进价）总计120万元．在销售过程中发现，年销售量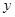
（万件）与销售单位
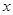（元）之间存在着如图所示的一次函数关系．
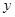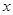（1）求关于的函数关系式；
（2）试写出该公司销售该种产品的年获利
（万元）关于销售单价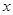（元）的函数关系式（年获利＝年销售额－年销售产品总进价－年总开支）．当销售单价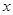为何值时，年获利最大？并求这个最大值；
（3）若公司希望该种产品一年的销售获利不低于40万元，借助（2）中函数的图象，请你帮助该公司确定销售单价的范围．在此情况下，要使产品销售量最大，你认为销售单价应定为多少元？
武警战士乘一冲锋舟从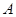
地逆流而上，前往
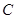地营救受困群众，途经
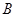地时，由所携带的救生艇将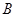地受困群众运回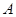地，冲锋舟继续前进，到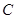地接到群众后立刻返回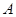地，途中曾与救生艇相遇．冲锋舟和救生艇距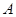地的距离
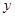（千米）和冲锋舟出发后所用时间
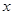之间的函数图象如图所示．假设营救群众的时间忽略不计，水流速度和冲锋舟在静水中的速度不变．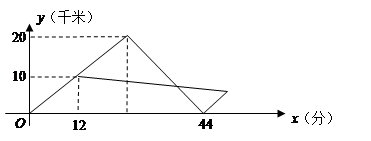
（1）请直接写出冲锋舟从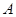地到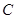地所用的时间．
（2）求水流的速度．
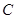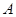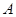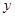（3）冲锋舟将地群众安全送到地后，又立即去接应救生艇．已知救生艇与地的距离（千米）和冲锋舟出发后所用时间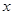之间的函数关系式为
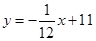，假设群众上下船的时间不计，求冲锋舟在距离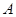地多远处与救生艇第二次相遇？
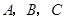三名大学生竞选系学生会主席，他们的笔试成绩和口试成绩（单位：分）分别用了两种方式进行了统计，如表一和图一：
表一
| A |
B |
C |
|
| 笔试 |
85 |
95 |
90 |
| 口试 |
80 |
85 |
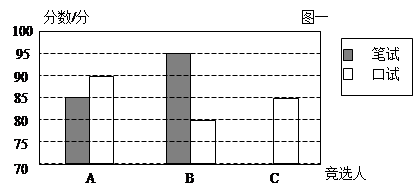
（1）请将表一和图一中的空缺部分补充完整．
（2）竞选的最后一个程序是由本系的300名学生进行投票，三位候选人的得票情况如图二（没有弃权票，每名学生只能推荐一个），请计算每人的得票数．
（3）若每票计1分，系里将笔试、口试、得票三项测试得分按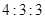
的比例确定个人成绩，请计算三位候选人的最后成绩，并根据成绩判断谁能当选．
有一底角为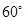
的直角梯形，上底长为10cm，与底垂直的腰长为10cm，以上底或与底垂直的腰为一边作三角形，使三角形的另一边长为15cm，第三个顶点落在下底上．请计算所作的三角形的面积．
如图，方格纸中每个小正方形的边长都是单位1．
（1）平移已知直角三角形，使直角顶点与点
重合，画出平移后的三角形．
（2）将平移后的三角形绕点逆时针旋转
，画出旋转后的图形．
（3）在方格纸中任作一条直线作为对称轴，画出（1）和（2）所画图形的轴对称图形，得到一个美丽的图案．
先化简：
，再任选一个你喜欢的数代入求值．