如图,已知矩形ABCD中, ,
,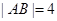 .将矩形ABCD沿对角线BD折起,使得面BCD⊥面ABD.现以D为原点,DB作为y轴的正方向,建立如图空间直角坐标系,此时点A恰好在xDy坐标平面内.试求A,C两点的坐标.
.将矩形ABCD沿对角线BD折起,使得面BCD⊥面ABD.现以D为原点,DB作为y轴的正方向,建立如图空间直角坐标系,此时点A恰好在xDy坐标平面内.试求A,C两点的坐标.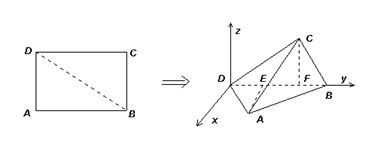
过直线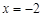 上的动点
上的动点 作抛物线
作抛物线 的两条切线
的两条切线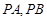 ,其中
,其中 为切点.
为切点.
⑴若切线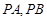 的斜率分别为
的斜率分别为 ,求证:
,求证: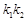 为定值;
为定值;
⑵求证:直线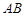 恒过定点.
恒过定点.
(本小题满分10分)
某校高一、高二两个年级进行乒乓球对抗赛,每个年级选出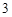 名学生组成代表队,比赛规则是:①按“单打、双打、单打”顺序进行三盘比赛;②代表队中每名队员至少参加一盘比赛,但不能参加两盘单打比赛.若每盘比赛中高一、高二获胜的概率分别为
名学生组成代表队,比赛规则是:①按“单打、双打、单打”顺序进行三盘比赛;②代表队中每名队员至少参加一盘比赛,但不能参加两盘单打比赛.若每盘比赛中高一、高二获胜的概率分别为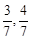 .
.
⑴按比赛规则,高一年级代表队可以派出多少种不同的出场阵容?
⑵若单打获胜得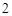 分,双打获胜得
分,双打获胜得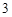 分,求高一年级得分
分,求高一年级得分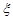 的概率发布列和数学期望.
的概率发布列和数学期望.
选修4—5:不等式选讲
已知正数a,b,c满足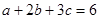 ,求证:
,求证: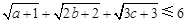 .
.
选修4-4:坐标系与参数方程(本小题满分10分)
在极坐标系中,已知曲线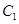 :
: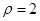 与曲线
与曲线 :
: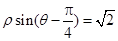 交于不同的两点
交于不同的两点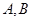 ,求
,求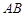 的值.
的值.
选修4—2:矩阵与变换 (本小题满分10分)
已知矩阵 ,
,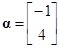 ,试计算:
,试计算: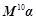 .
.