(本小题满分12分)已知 ,设函数
,设函数 .
.
(Ⅰ)若 在
在 上无极值,求
上无极值,求 的值;
的值;
(Ⅱ)若存在 ,使得
,使得 是
是 在[0, 2]上的最大值,求t的取值范围;
在[0, 2]上的最大值,求t的取值范围;
(Ⅲ)若 (
( 为自然对数的底数)对任意
为自然对数的底数)对任意 恒成立时m的最大值为1,求t的取值范围.
恒成立时m的最大值为1,求t的取值范围.
(本小题满分12分)如图,抛物线 :
: 与椭圆
与椭圆 :
: 在第一象限的交点为
在第一象限的交点为 ,
, 为坐标原点,
为坐标原点, 为椭圆的右顶点,
为椭圆的右顶点, 的面积为
的面积为 .
.
(Ⅰ)求抛物线 的方程;
的方程;
(Ⅱ)过 点作直线
点作直线 交
交 于
于 、
、 两点,射线
两点,射线 、
、 分别交
分别交 于
于 、
、 两点,记
两点,记 和
和 的面积分别为
的面积分别为 和
和 ,问是否存在直线
,问是否存在直线 ,使得
,使得 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(本小题满分12分)如图,在 中,已知
中,已知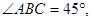
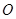 在
在 上,且
上,且 又
又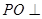 平面
平面 .
.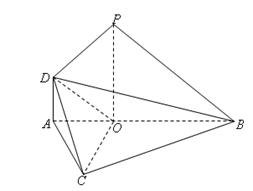
(Ⅰ)求证: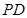 ⊥平面
⊥平面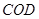 ;
;
(Ⅱ)求二面角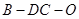 的余弦值.
的余弦值.
(本小题满分12分)根据以往的经验,某工程施工期间的降水量X(单位:mm)对工期的影响如下表:
| 降水量X |
X<300 |
300≤X<700 |
700≤X<900 |
X≥900 |
| 工期延 |
||||
| 误天数Y |
0 |
2 |
6 |
10 |
历年气象资料表明,该工程施工期间降水量X小于300,700,900的概率分别为0.3 ,0.7 ,0.9.求:
(Ⅰ)工期延误天数Y的均值与方差;
(Ⅱ)在降水量X至少是300的条件下,工期延误不超过6天的概率.
(本小题满分 分)在
分)在 中,角
中,角 所对的边为
所对的边为 ,且满足
,且满足 .
.
(Ⅰ)求角 的值;
的值;
(Ⅱ)若 且
且 ,求
,求 的取值范围.
的取值范围.