（本小题满分12分）根据以往的经验，某工程施工期间的降水量X（单位：mm）对工期的影响如下表：
| 降水量X |
X<300 |
300≤X<700 |
700≤X<900 |
X≥900 |
| 工期延 |
|
|
|
|
| 误天数Y |
0 |
2 |
6 |
10 |
历年气象资料表明，该工程施工期间降水量X小于300,700,900的概率分别为0．3 ,0．7 ,0．9．求：
（Ⅰ）工期延误天数Y的均值与方差；
（Ⅱ）在降水量X至少是300的条件下，工期延误不超过6天的概率．
（本小题满分12分）已知
（1）求函数
的最小正周期及在区间
的最大值;
（2）在
中,
所对的边分别是
，
，
求
周长
的最大值.
（本小题满分10分）等差数列
中，
，公差
且
成等比数列，前
项的和为
.
（1）求
及;
（2）设
，
，求
.
已知集合A＝{x|2≤x≤8}，B＝{x|1<x<6}，C＝{x|x>a}，U＝R.
（1）求A∪B，（∁UA）∩B；
（2）若A∩C≠∅，求a的取值范围．
证明：（1）对任一正整
，都存在整数
，使得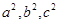
成等差数列。
（2）存在无穷多个互不相似的三角形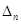
，其边长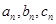
为正整数且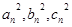
成等差数列。
已知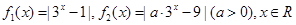
,
且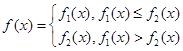
.
（Ⅰ）当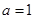
时,求
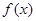在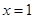
处的切线方程；
（Ⅱ）当
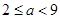时,设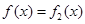
所对应的自变量取值区间的长度为
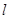（闭区间
的长度定义为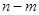
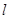）,试求的最大值；
（Ⅲ）是否存在这样的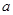
，使得当
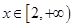时,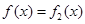?若存在,求出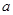的取值范围；若不存在，请说明理由.