(本小题满分13分)
随机调查某社区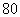 个人,以研究这一社区居民在
个人,以研究这一社区居民在 时间段的休闲方
时间段的休闲方
式与性别的关系,得到下面的数据表:
| 休闲方式 性别 |
看电视 |
看书 |
合计 |
| 男 |
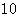 |
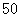 |
 |
| 女 |
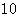 |
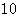 |
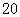 |
| 合计 |
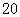 |
 |
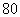 |
(1)将此样本的频率估计为总体的概率,随机调查 名在该社区的男性,设调查的
名在该社区的男性,设调查的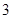 人
人
在这一时间段以看书为休闲方式的人数为随机变量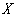 ,求
,求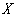 的分布列和期望;
的分布列和期望;
(2)根据以上数据,能否有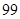 %的把握认为“在
%的把握认为“在 时间段的休闲方式与
时间段的休闲方式与
性别有关系”?
参考公式: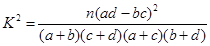 ,其中
,其中 .
.
参考数据:
 |
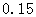 |
 |
 |
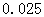 |
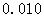 |
 |
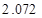 |
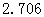 |
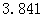 |
 |
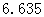 |
已知函数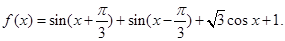
(Ⅰ)若 求
求 的值域;
的值域;
(Ⅱ)△ABC中,角A,B,C的对边为a,b,c,若 求
求 的值.
的值.
设函数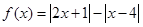 .
.
(I)解不等式 ;
;
(II)求函数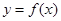 的最小值.
的最小值.
平面直角坐标系中,直线 的参数方程是
的参数方程是 (
( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的正半轴为极轴,建立极坐标系,已知曲线
轴的正半轴为极轴,建立极坐标系,已知曲线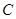 的极坐标方程为
的极坐标方程为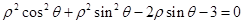 .
.
(Ⅰ)求直线 的极坐标方程;
的极坐标方程;
(Ⅱ)若直线 与曲线
与曲线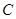 相交于
相交于 两点,求
两点,求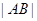 .
.
如图,C是以AB为直径的半圆O上的一点,过C的直线交直线AB于E,交过A点的切线于D,BC∥OD.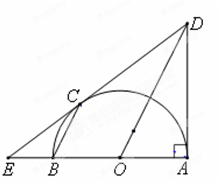
(Ⅰ)求证:DE是圆O的切线;
(Ⅱ)如果AD=AB=2,求EB.
已知椭圆C: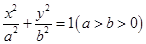 的离心率为
的离心率为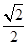 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线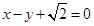 相切.
相切.
(1)求椭圆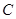 的方程;
的方程;
(2)若过点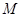 (2,0)的直线与椭圆
(2,0)的直线与椭圆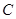 相交于两点
相交于两点 ,设
,设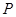 为椭圆上一点,且满足
为椭圆上一点,且满足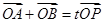 (
(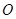 为坐标原点),当
为坐标原点),当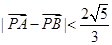 时,求实数
时,求实数 取值范围.
取值范围.