已知椭圆 ,椭圆
,椭圆 以
以 的长轴为短轴,且与
的长轴为短轴,且与 有相同的离心率.
有相同的离心率.
(1)求椭圆 的方程;
的方程;
(2)设 为坐标原点,点
为坐标原点,点 、
、 分别在椭圆
分别在椭圆 和
和 上,
上, ,求直线
,求直线 的方程.
的方程.
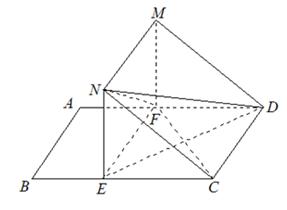
如图,矩形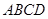 中,
中,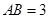 ,
,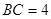 .
.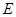 ,
,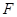 分别在线段
分别在线段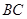 和
和 上,
上,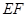 ∥
∥ ,将矩形
,将矩形 沿
沿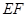 折起.记折起后的矩形为
折起.记折起后的矩形为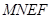 ,且平面
,且平面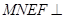 平面
平面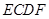 .
.
(Ⅰ)求证: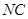 ∥平面
∥平面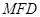 ;
;
(Ⅱ)若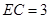 ,求证:
,求证: ;
;
(Ⅲ)求四面体 体积的最大值.
体积的最大值.
现对某市工薪阶层关于“楼市限购政策”的态度进行调查,随机抽查了50人,他们月收入(单位:百元)的频数分布及对“楼市限购政策”赞成人数如下表:
| 月收入(单位百元) |
[15,25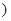 |
[25,35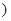 |
[35,45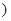 |
[45,55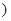 |
[55,65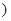 |
[65,75 |
| 频数 |
5 |
10 |
15 |
10 |
5 |
5 |
| 赞成人数 |
4 |
8 |
12 |
5 |
2 |
1 |
(Ⅰ)根据以上统计数据填写下面2×2列联表,并回答是否有99%的把握认为月收入以5500元为分界点对“楼市限购政策” 的态度有差异?
| 月收入不低于55百元的人数 |
月收入低于55百元的人数 |
合计 |
|
| 赞成 |
 |
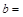 |
|
| 不赞成 |
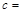 |
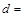 |
|
| 合计 |
(Ⅱ)若从月收入在[55,65)的被调查对象中随机选取两人进行调查,求至少有一人不赞成“楼市限购政策”的概率.
(参考公式: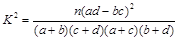 ,其中
,其中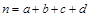 .)
.)
参考值表:
P( ) ) |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
已知函数 .
.
(Ⅰ)求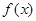 的单调递增区间;
的单调递增区间;
(Ⅱ)在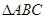 中,角
中,角 ,
,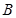 ,
,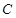 的对边分别为
的对边分别为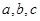 .已知
.已知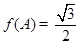 ,
,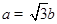 ,试判断
,试判断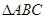 的形状.
的形状.
甲、乙、丙三人独立破译同一份密码,已知甲、乙、丙各自破译出密码的概率分别为 .且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为
.且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为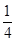 .
.
(Ⅰ)求甲乙二人中至少有一人破译出密码的概率;
(Ⅱ)求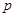 的值;
的值;
(Ⅲ)设甲、乙、丙三人中破译出密码的人数为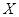 ,求
,求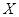 的分布列和数学期望
的分布列和数学期望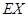 .
.
已知数列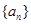 中,
中,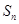 是
是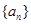 的前
的前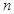 项和,且
项和,且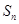 是
是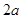 与
与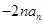 的等差中项,其中
的等差中项,其中 是不等于零的常数.
是不等于零的常数.
(1)求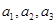 ; (2)猜想
; (2)猜想 的表达式,并用数学归纳法加以证明.
的表达式,并用数学归纳法加以证明.