一汽车厂生产 、
、 、
、 三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆)
三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆)
| |
轿车 |
轿车 |
轿车 |
| 舒适型 |
 |
 |
 |
| 标准型 |
 |
 |
 |
按类型分层抽样的方法在这个月生产的轿车中抽取 辆,其中有
辆,其中有 类轿车
类轿车 辆.
辆.
(1)求 的值;
的值;
(2)用分层抽样的方法在 类轿车中抽取一个容量为
类轿车中抽取一个容量为 的样本.将该样本看成一个总体,从中任取
的样本.将该样本看成一个总体,从中任取 辆,求至少有
辆,求至少有 辆舒适型轿车的概率;
辆舒适型轿车的概率;
(3)用随机抽样的方法从 类舒适型轿车中抽取
类舒适型轿车中抽取 辆,经检测它们的得分如下:
辆,经检测它们的得分如下: 、
、 、
、 、
、 、
、 、
、 、
、 、
、 .把这
.把这 辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值
辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值
不超过 的概率.
的概率.
(本小题满分12分)
已知函数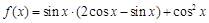 .
.
(Ⅰ)求函数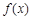 的最小正周期;
的最小正周期;
(Ⅱ)设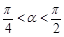 ,且
,且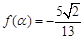 ,求
,求 的值.
的值.
(本题满分18分)本题共3小题,第(1)小题6分,第(2)小题6分,第(3)小题6分.
已知函数 .
. 
(1)指出 的基本性质(结论不要求证明)并作出函数
的基本性质(结论不要求证明)并作出函数 的图像;
的图像;
(2)关于 的不等式
的不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)关于 的方程
的方程 (
( )恰有6个不同的实数解,求
)恰有6个不同的实数解,求 的取值范围.
的取值范围.
(本题满分16分)本题共3小题,第(1)小题4分,第(2)小题4分,第(3)小题8分.
已知数列 是公差不为
是公差不为 的等差数列,
的等差数列, 数列
数列 是等比数列,且
是等比数列,且 ,
, ,数列
,数列 的前
的前 项和为
项和为 ,记点
,记点 .
.
(1)求数列 的通项公式;
的通项公式;
(2)证明:点 在同一直线
在同一直线 上,并求出直线
上,并求出直线 方程;
方程;
(3)若 对
对 恒成立,求
恒成立,求 的最小值.
的最小值.
(本题满分14分)本题共2小题,第(1)小题6分,第(2)小题8分.
如图所示的“8”字形曲线是由两个关于 轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是
轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是 ,双曲线的左、右顶点
,双曲线的左、右顶点 、
、 是该圆与
是该圆与 轴的交点,双曲线与半圆相交于与
轴的交点,双曲线与半圆相交于与 轴平行的直径的两端点.
轴平行的直径的两端点.
(1)试求双曲线的标准方程;
(2)记双曲线的左、右焦点为 、
、 ,试在“8”字形曲线上求点
,试在“8”字形曲线上求点 ,使得
,使得 是直角.
是直角.
(本题满分14分)本题共2小题,第(1)小题8分,第(2)小题6分.
如图,摩天轮上一点 在
在 时刻距离地面高度满足
时刻距离地面高度满足 ,
, ,已知某摩天轮的半径为
,已知某摩天轮的半径为 米,点
米,点 距地面的高度为
距地面的高度为 米,摩天轮做匀速转动,每
米,摩天轮做匀速转动,每 分钟转一圈,点
分钟转一圈,点 的起始位置在摩天轮的最低点处.
的起始位置在摩天轮的最低点处.
(1)根据条件写出 (米)关于
(米)关于 (分钟)的解析式;
(分钟)的解析式;
(2)在摩天轮转动的一圈内,有多长时间点 距离地面超过
距离地面超过 米?
米?