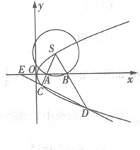
李先生是一家快餐店的经理,下面是该快餐店所有工作人员8月份的工资表:
| 李某 |
大厨 |
二厨 |
采购员 |
杂工 |
服务员 |
会计 |
| 3000元 |
450元 |
350元 |
400元 |
320元 |
320元 |
410元 |
(1)计算所有人员8月份的平均工资;
(2)计算出平均工资能反映打工人员这个月收入的一般水平吗?
(3)去掉李某工资后,再计算剩余人员的平均工资,这能代表一般打工人员当月的收入水平吗?
(本小题满分14分)设等差数列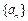 的前
的前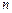 项和为
项和为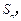 且
且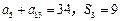 .
.
(1)求数列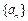 的通项公式及前
的通项公式及前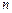 项和公式;
项和公式;
(2)设数列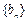 的通项公式为
的通项公式为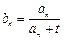 ,问: 是否存在正整数t,使得
,问: 是否存在正整数t,使得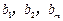
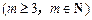 成等差数列?若存在,求出t和m的值;若不存在,请说明理由.
成等差数列?若存在,求出t和m的值;若不存在,请说明理由.
(本小题满分14分)如图,已知AB⊥平面ACD,DE⊥平面ACD,AC=AD,
DE=2AB,F为CD的中点.
(1)求证:AF∥平面BCE;(2)求证:平面BCE⊥平面CDE.
(本小题满分14分)
如图,过原点且倾斜角为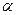 的直线交单位圆于点
的直线交单位圆于点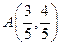 ,C是单位圆与
,C是单位圆与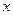 轴正半轴的交点,B是单位圆上第二象限的点,且
轴正半轴的交点,B是单位圆上第二象限的点,且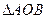 为正三角形。
为正三角形。
(I)求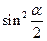 的值;
的值;
(II)求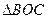 的面积。
的面积。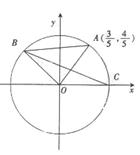
(本题15分) 已知函数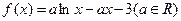 .
.
(Ⅰ)当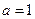 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅱ)若函数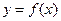 的图像在点
的图像在点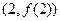 处的切线的倾斜角为
处的切线的倾斜角为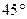 ,问:m在什么范围取值时,对于任意的
,问:m在什么范围取值时,对于任意的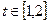 ,函数
,函数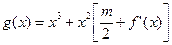 在区间
在区间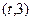 上总存在极值?
上总存在极值?
(Ⅲ)当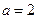 时,设函数
时,设函数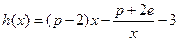 ,若在区间
,若在区间 上至少存在一个
上至少存在一个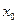 ,使得
,使得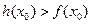 成立,试求实数p的取值范围.
成立,试求实数p的取值范围.
(本题15分)如图,S(1,1)是抛物线为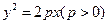 上的一点,弦SC,SD分别交
上的一点,弦SC,SD分别交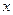 轴于A,B两点,且SA=SB。
轴于A,B两点,且SA=SB。
(I)求证:直线CD的斜率为定值;
(Ⅱ)延长DC交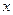 轴于点E,若
轴于点E,若 ,求
,求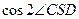 的值。
的值。