（本小题满分12分）已知函数
，
，
（1） 判断函数
的奇偶性，并证明；
（2） 判断的单调性,并说明理由。（不需要严格的定义证明,只要说出理由即可）
（3） 若
，方程
是否有根？如果有根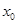
，请求出一个长度为1的区间
，使
；如果没有，请说明理由。（注：区间的长度＝
）
设p:y=(x2-4)(x-a)在(-∞,-2)和(2,+∞）上是单调增函数；q:不等式
(2t-2)dt＞a的解集为R.如果p与q有且只有一个正确，求a的取值范围.
在区间［0，1］上给定曲线y=x2，试在此区间内确定点t的值，使图中阴影部分的面积S1与S2之和最小.
如图所示，抛物线y=4-x2与直线y=3x的两交点为A、B，点P在抛物线上从A向B运动.
（1）求使△PAB的面积最大的P点的坐标(a,b);
(2)证明由抛物线与线段AB围成的图形，被直线x=a分为面积相等的两部分.
设函数f(x)=x3+ax2+bx在点x=1处有极值-2.
（1）求常数a,b的值；
（2）求曲线y=f(x)与x轴所围成的图形的面积.
证明：把质量为m（单位：kg）的物体从地球的表面升高h(单位：m)处所做的功W=G·
，其中G是地球引力常数，M是地球的质量，k是地球的半径.