设 是定义在
是定义在 上的函数,且对任意
上的函数,且对任意 ,当
,当 时,都有
时,都有 ;
;
(1)当 时,比较
时,比较 的大小;
的大小;
(2)解不等式 ;
;
(3)设 且
且 ,求
,求 的取值范围。
的取值范围。
若实数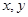 满足
满足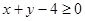 ,则
,则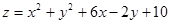 的最小值为_______.
的最小值为_______.
(本小题满分14分)已知函数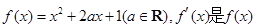 的导函数.
的导函数.
(1)若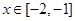 ,不等式
,不等式 恒成立,求a的取值范围;
恒成立,求a的取值范围;
(2)解关于x的方程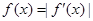 ;
;
(3)设函数 ,求
,求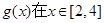 时的最小值.
时的最小值.
(本小题满分14分)已知直线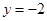 上有一个动点
上有一个动点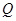 ,过点
,过点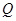 作直线
作直线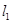 垂直于
垂直于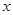 轴,动点
轴,动点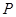 在
在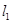 上,且满足
上,且满足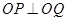 (
(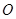 为坐标原点),记点
为坐标原点),记点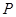 的轨迹为
的轨迹为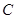 .
.
(1)求曲线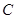 的方程;
的方程;
(2)若直线 是曲线
是曲线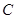 的一条切线,当点
的一条切线,当点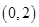 到直线
到直线 的距离最短时,求直线
的距离最短时,求直线 的方程.
的方程.
(本小题满分14分)已知递增等差数列 中的
中的 是函数
是函数 的两个零点.数列
的两个零点.数列 满足,点
满足,点 在直线
在直线 上,其中
上,其中 是数列
是数列 的前
的前 项和.
项和.
(1)求数列 和
和 的通项公式;
的通项公式;
(2)令 ,求数列
,求数列 的前n项和
的前n项和 .
.
(本小题满分14分)如图,在直三棱柱 中,
中, ,
, 、
、 分别是
分别是 ,
, 的中点.
的中点.
(1)求证: ∥平面
∥平面 ;
;
(2)求证:平面 平面
平面 ;
;
(3)若 ,
, ,求三棱锥
,求三棱锥 的体积.
的体积.