(本小题满分14分)已知直线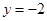 上有一个动点
上有一个动点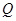 ,过点
,过点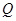 作直线
作直线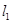 垂直于
垂直于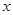 轴,动点
轴,动点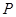 在
在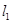 上,且满足
上,且满足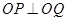 (
(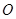 为坐标原点),记点
为坐标原点),记点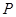 的轨迹为
的轨迹为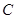 .
.
(1)求曲线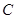 的方程;
的方程;
(2)若直线 是曲线
是曲线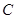 的一条切线,当点
的一条切线,当点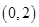 到直线
到直线 的距离最短时,求直线
的距离最短时,求直线 的方程.
的方程.
已知圆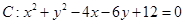 的圆心在点
的圆心在点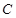 ,点
,点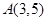 ,求;
,求;
(1)过点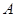 的圆的切线方程;
的圆的切线方程;
(2)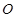 点是坐标原点,连结
点是坐标原点,连结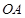 ,
,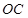 ,求
,求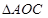 的面积
的面积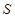 .
.
设 :“
:“
 ”,
”, :“函数
:“函数
 在
在 上的值域为
上的值域为 ”,若“
”,若“ ”是假命题,求实数a的取值范围.
”是假命题,求实数a的取值范围.
已知偶函数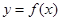 满足:当
满足:当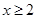 时,
时,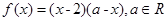 ,当
,当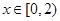 时,
时, .
.
(Ⅰ).求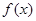 表达式;
表达式;
(Ⅱ).若直线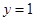 与函数
与函数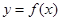 的图像恰有两个公共点,求实数
的图像恰有两个公共点,求实数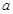 的取值范围;
的取值范围;
(Ⅲ).试讨论当实数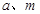 满足什么条件时,直线
满足什么条件时,直线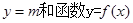 的图像恰有
的图像恰有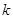 个公共点
个公共点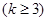 ,且这
,且这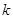 个公共点均匀分布在直线
个公共点均匀分布在直线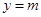 上.(不要求过程)
上.(不要求过程)
如图,斜率为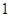 的直线过抛物线
的直线过抛物线 的焦点,与抛物线交于两点A、B, M为抛物线弧AB上的动点.
的焦点,与抛物线交于两点A、B, M为抛物线弧AB上的动点.
(Ⅰ).若 ,求抛物线的方程;
,求抛物线的方程;
(Ⅱ).求△ABM面积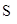 的最大值.
的最大值.
已知函数
(Ⅰ).求函数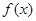 的单调区间及
的单调区间及 的取值范围;
的取值范围;
(Ⅱ).若函数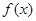 有两个极值点
有两个极值点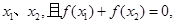 求
求 的值.
的值.