(本小题满分8分)
已知集合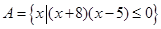 ,
, 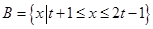 .若
.若 ,求实数
,求实数 的取值范围.
的取值范围.
(本小题满分16分:4+5+7)
已知函数 ,其中e为常数,
,其中e为常数,
(e=2.71828...),
(1)当a=1时,求 的单调区间与极值;
的单调区间与极值;
(2)求证:在(1)的条件下,
(3)是否存在实数 ,使
,使 最小值为3,若存在,求出
最小值为3,若存在,求出 的值,若不存在,说明理由。
的值,若不存在,说明理由。
(本小题满分16分:8+8)
给出函数封闭的定义:若对于定义域D内的任一个自变量 ,都有函数值
,都有函数值 ,则称函数y=f(x)在 D上封闭。
,则称函数y=f(x)在 D上封闭。
(1)若定义域 判断下列函数中哪些在
判断下列函数中哪些在 上封闭,并给出推理过程;
上封闭,并给出推理过程;
(2)若定义域 是否存在实数
是否存在实数 ,使函数
,使函数 在
在 上封闭,若存在,求出
上封闭,若存在,求出 值,若不存在,请说明理由。
值,若不存在,请说明理由。
(本小题满分16分:4+5+7)
已知O为坐标原点,向量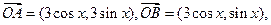
 ,
,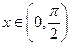
(1)求证: ;
;
(2)若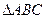 是等腰三角形,求x;
是等腰三角形,求x;
(3)求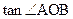 的最大值及相应的x值。
的最大值及相应的x值。
(本小题满分14分:6+8)
某投资公司投资甲、乙两个项目所得的利润分别是P(亿元)和Q(亿元),它们与投资额t(亿元)的关系有经验公式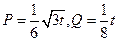 ,今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所得的总利润为y(亿元)
,今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所得的总利润为y(亿元)
(1)求y关于x的函数表达式;
(2)求总利润的最大值。
(本小题满分14分:8+6)
已知不等式 的解集为A,不等式
的解集为A,不等式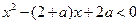 的解集为B
的解集为B
(1)求集合A及B;
(2)若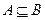 ,求实数a的取值范围。
,求实数a的取值范围。