(本小题14分)设各项为正的数列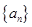 的前
的前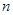 项和为
项和为
且满足:
(1)求
(2)若 ,求
,求
(本小题满分12分)已知 ,
,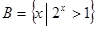 ,
,
(1)求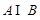 和
和 ;
;
(2)若记符号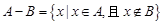 ,
,
①在图中把表示“集合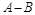 ”的部分用阴影涂黑;
”的部分用阴影涂黑;
②求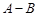 和
和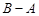 .
.
(本小题满分15分)设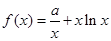 ,
,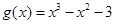 .
.
(1)当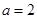 时,求曲线
时,求曲线 在
在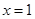 处的切线的斜率;
处的切线的斜率;
(2)如果存在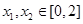 ,使得
,使得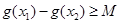 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数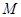 ;
;
(3)如果对于任意 ,都有
,都有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(本小题满分15分)已知函数 ,
,
(1)若 ,且
,且 的取值范围
的取值范围
(2)当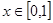 时,
时, 恒成立,且
恒成立,且 的取值范围
的取值范围
数列 的前
的前 项和为
项和为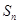 ,
, ,
,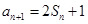 ,等差数列
,等差数列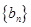 满足
满足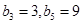 ,
,
(I)分别求数列 ,
,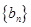 的通项公式;
的通项公式;
(II)若对任意的 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
若向量 ,
, 其中
其中 ,记函数
,记函数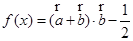 ,若函数
,若函数 的图像与直线
的图像与直线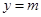 (
( 为常数)相切,并且切点的横坐标依次成公差为
为常数)相切,并且切点的横坐标依次成公差为 的等差数列。
的等差数列。
(1)求 的表达式及
的表达式及 的值;
的值;
(2)将函数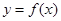 的图像向左平移
的图像向左平移 ,得到
,得到 的图像,当
的图像,当 时,
时,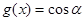 的交点横坐标成等比数列,求钝角
的交点横坐标成等比数列,求钝角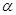 的值。
的值。