某校要用三辆汽车从新校区把教职工接到老校区,已知从新校区到老校区有两条公路,汽车走公路①堵车的概率为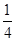 ,不堵车的概率为
,不堵车的概率为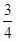 ;汽车走公路②堵车的概率为
;汽车走公路②堵车的概率为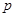 ,不堵车的概率为
,不堵车的概率为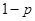 .若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响
.若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响 .(Ⅰ)若三辆汽车中恰有一辆汽车被堵
.(Ⅰ)若三辆汽车中恰有一辆汽车被堵 的概率为
的概率为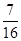 ,求走公路②堵车的概率;
,求走公路②堵车的概率;
(Ⅱ)在(Ⅰ)的条件下,求三辆汽车中被堵车辆的个数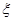 的分布列和数学期望。
的分布列和数学期望。
设锐角△ABC的 三内角A,B,C的对边分别为a,b,c,向量
三内角A,B,C的对边分别为a,b,c,向量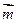
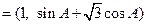 ,
,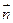
 ,已知
,已知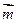 与
与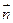 共线。(Ⅰ)求角A的大小;
共线。(Ⅰ)求角A的大小;
(Ⅱ)若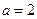 ,
,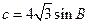 ,且△ABC的面积小于
,且△ABC的面积小于 ,求角B的取值范围。
,求角B的取值范围。
(本题满分14分)
已知点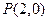 及圆
及圆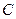 :
: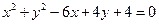 .
.
(Ⅰ)若直线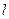 过点
过点 且与圆心
且与圆心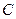 的距离为1,求直线
的距离为1,求直线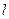 的方程;
的方程;
(Ⅱ)设过 直线
直线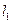 与圆
与圆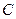 交于
交于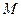 、
、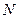 两点,当
两点,当 时,求以
时,求以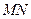 为直径的圆的方程;
为直径的圆的方程;
(Ⅲ)设直线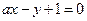 与圆
与圆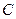 交于
交于 ,
,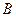 两点,是否存在实数
两点,是否存在实数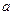 ,使得过点
,使得过点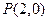 的直线
的直线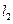 垂直平分
垂直平分 弦
弦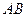 ?若存在,求出实数
?若存在,求出实数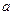 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本题满分12分)
如图,已知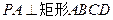 所在的平面,
所在的平面, 分别为
分别为 的中点,
的中点,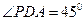 ,
,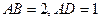
(Ⅰ)求证: ;
;
(Ⅱ)求证: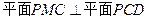 ;
;
(Ⅲ)求三棱锥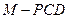 的体积.
的体积.
(本题满分12分)
已知二次函数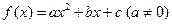 满足
满足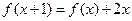 且
且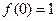 .
.
(Ⅰ)求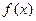 的解析式;
的解析式;
(Ⅱ)当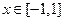 时,不等式:
时,不等式: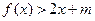 恒成立,求实数
恒成立,求实数 的范围.
的范围.