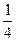(本小题满分12分)设某物体一天中的温度 是时间
是时间 的函数:
的函数: ,其中温度的单位是
,其中温度的单位是 ,时间单位是小时,
,时间单位是小时, 表示12:00,
表示12:00, 取正值表示12:00以后.若测得该物体在8:00的温度是
取正值表示12:00以后.若测得该物体在8:00的温度是 ,12:00的温度为
,12:00的温度为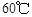 ,13:00的温度为
,13:00的温度为 ,且已知该物体的温度在8:00和16:00有相同的变化率.
,且已知该物体的温度在8:00和16:00有相同的变化率.
(1)写出该物体的温度 关于时间
关于时间 的函数关系式;
的函数关系式;
(2)该物体在10:00到14:00这段时间中(包括10:00和14:00),何时温度最高,并求出最高温度;
(3)如果规定一个函数 在区间
在区间 上的平均值为
上的平均值为 ,求该物体在8:00到16:00这段时间内的平均温度.
,求该物体在8:00到16:00这段时间内的平均温度.
四 附加题:(本小题满分15分)
已知函数 (
( 为自然对数的底数).a
为自然对数的底数).a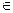 R
R
( 1)当a=1时,求函数
1)当a=1时,求函数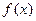 的最小值;
的最小值;
(2)若函数f(x)在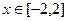 上存在极小值,求a的取值范围;
上存在极小值,求a的取值范围;
(3)若 ,证明:
,证明: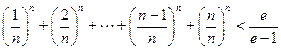 .
.
(本小题12分)
已知函数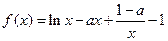
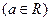 .
.
(Ⅰ)当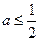 时,讨论
时,讨论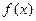 的单调性;
的单调性;
(Ⅱ)设 当
当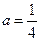 时,若对任意
时,若对任意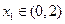 ,存在
,存在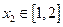 ,使
,使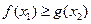 ,求实数
,求实数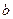 取值范围.
取值范围.
(本小题12分)
已知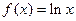 ,
, ,直线
,直线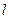 与函数
与函数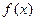 、
、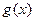 的图象都相切,且与函数
的图象都相切,且与函数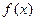 的图象的切点的横坐标为
的图象的切点的横坐标为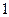 .
.
(Ⅰ)求直线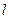 的方程及
的方程及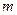 的值;
的值;
(Ⅱ)若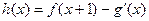 ,求函数
,求函数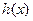 的最大值;
的最大值;
(Ⅲ)当 时,求证:
时,求证: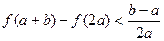 .
.
(本小题12分)
已知数列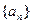 的前项和为
的前项和为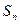 ,
,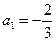 ,
,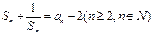
(1)求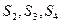
(2)猜想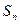 的表
的表 达式,并用数学归纳法证明。
达式,并用数学归纳法证明。
(本小题12分)
已知a,b,c∈(0,1),求证:(1-a)b, (1-b)c, (1-c)a.不能同时大于