在一个不透明的盒子里装有只有颜色不同的黑、白两种球共50个，林林做摸球实验，他将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是实验中的一组统计数据：
摸球的次数 |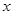
100 |
200 |
300 |
500 |
800 |
1000 |
3000 |
摸到白球的次数 |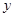
64 |
122 |
177 |
301 |
470 |
592 |
1802 |
摸到白球的频率 |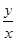
0.63 |
0.61 |
0.590 |
0.602 |
0.588 |
0.592 |
0.601 |
（1）请估计：当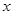很大时，摸到白球的频率将会接近 ．（精确到0.1）
（2）假如你摸一次，你摸到白球的概率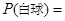
．
（3）试估算盒子里黑、白两种颜色的球各有多少只？
设计一个商标图案（如图阴影部分），其中O为半圆的圆心，AB＝a，BC＝b，
（1）用关于a，b的代数式表示商标图案的面积S；
（2）求当a＝6cm，b＝4cm时S的值．（本题结果都保留π）
解方程：
（1）8-5x=x＋2
（2）y－
=2－
计算：
（1）
；
（2）
（用简便方法）．
某织布厂有工人200名，为改善经营，增设制衣项目，已知每人每天能织布30米，或利用所织布制衣4件，制衣一件用布1．5米，将布直接出售，每米布可获利2元；将布制成衣后出售，每件可获利25元，若每名工人一天只能做一项工作，且不计其他因素，设安排x名工人制衣，那么：
（1）一天中制衣所获得的利润为P=___________________（试用含x的代数式表示并化简）；
（2）一天中剩余布出售所获利润为Q=________________（试用含x的代数式表示并化简）；
（3）当安排166名工人制衣时，所获总利润是多少元?能否安排167名工人制衣以提高利润? 试说明理由．
某中学为了了解本校学生的每周课外阅读时间，采用随机抽样的方式进行了问卷调查，调查结果分为“2小时以内”、“2小时～3小时”、“3小时～4小时”和“4小时以上”四个等级，分别用A、B、C、D表示，根据调查结果绘制成了如图所示的两幅不完整的统计图．由图中所给出的信息解答下列问题：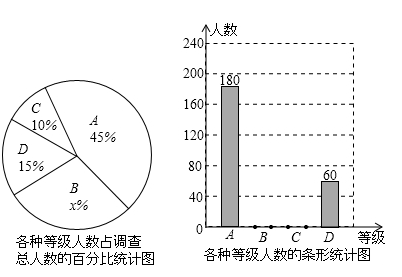
（1）求出x的值，并将不完整的条形图补充完整；
（2）若学校有学生1200人，请你估计每周课外阅读时间在“2小时～3小时”的有多少人？