某教授为了测试贫困地区和发达地区的同龄儿童的智力,出了10个智力题,每个题10分,然后作了统计,结果如下:
贫困地区
| 参加测试的人数 |
30 |
50 |
100 |
200 |
500 |
800 |
| 得60分以上的人数 |
16 |
27 |
52 |
104 |
256 |
402 |
| 得60分以上的频率 |
|
|
|
|
|
|
发达地区
| 参加测试的人数 |
30 |
50 |
100 |
200 |
500 |
800 |
| 得60分以上的人数 |
17 |
29 |
56 |
111 |
276 |
440 |
| 得60分以上的频率 |
|
|
|
|
|
|
(1)计算两地区参加测试的儿童得60分以上的频率;
(2)求两个地区参加测试的儿童得60分以上的概率;
(3)分析贫富差距为什么会带来人的智力的差别.
求使等式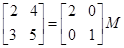 成立的矩阵
成立的矩阵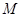 .
.
已知函数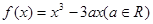
(1)当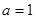 时,求
时,求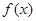 在
在 的最小值;
的最小值;
(2)若直线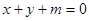 对任意的
对任意的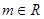 都不是曲线
都不是曲线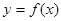 的切线,求
的切线,求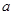 的取值范围;
的取值范围;
(3)设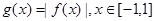 ,求
,求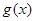 的最大值
的最大值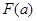 的解析式
的解析式
已知点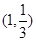 是函数
是函数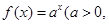 且
且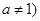 的图像上一点,等比数列
的图像上一点,等比数列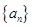 的前
的前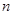 项的和为
项的和为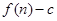 ;数列
;数列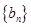
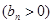 的首项为
的首项为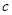 ,且前
,且前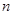 项和
项和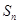 满足
满足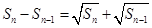
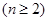 .
.
求数列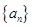 和
和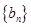 的通项公式;
的通项公式;
若数列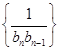 的前
的前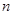 项和为
项和为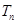 ,问
,问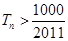 的最小正整数
的最小正整数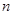 是多少?
是多少?
据行业协会预测:某公司以每吨10万元的价格销售某种化工产品,可售出该产品1000 吨,若将该产品每吨的价格上涨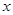 %,则销售量将减少
%,则销售量将减少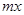 %,且该化工产品每吨的价格上涨幅度不超过
%,且该化工产品每吨的价格上涨幅度不超过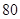 %,
%,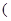 其中
其中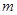 为正常数
为正常数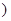

(1)当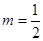 时,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
时,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
(2)如果涨价能使销售总金额比原销售总金额多,求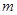 的取值范围.
的取值范围.
如图,在四棱锥 中,底面
中,底面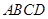 是正方形,侧面
是正方形,侧面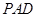
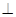 底面
底面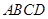 ,若
,若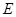 、
、 分别为
分别为 、
、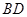 的中点.
的中点.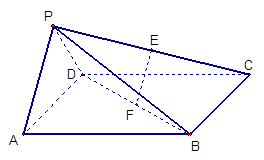
(Ⅰ) 求证: //平面
//平面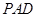 ;
;
(Ⅱ) 求证:平面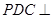 平面
平面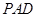 ;
;