(本题12分)如图,在侧棱锥垂直底面的四棱锥ABCD-A1B1C1D1中,AD∥BC,
AD⊥AB,AB= 。AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E
。AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E
与直线AA1的交点。
(1)证明:(i)EF∥A1D1;
(ii)BA1⊥平面B1C1EF;
(2)求BC1与平面B1C1EF所成的角的正弦值。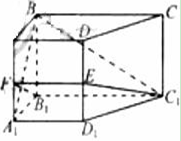
(本题8分)如图,ABCD是正方形,O是正方形的中心, PO 底面ABCD,E是PC的中点。
底面ABCD,E是PC的中点。
求证:(1)PA∥平面BDE(2)平面PAC 平面BDE
平面BDE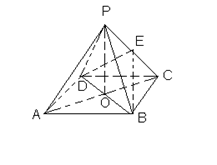
(本题6分)已知圆台的母线长为4 cm,母线与轴的夹角为30°,上底面半径是下底面半径的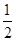 ,求这个圆台的侧面积.
,求这个圆台的侧面积.
(本题6分)已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8、高为4的等腰三角形,侧视图是一个底边长为6、高为4的等腰三角形.
(1)求该几何体的体积V;
(2)求该几何体的侧面积S。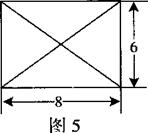
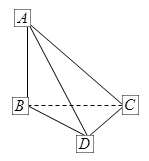
如图所示,在四面体 中,
中,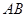 ,
,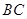 ,
, 两两互相垂直,且
两两互相垂直,且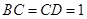 .
.
(1)求证:平面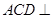 平面
平面 ;
;
(2)求二面角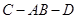 的大小;
的大小;
(3)若直线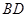 与平面
与平面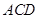 所成的角为
所成的角为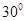 ,求线段
,求线段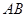 的长度.
的长度.