为了预防流感,某学校对教室用药熏消毒法进行消毒. 已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为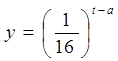 (a为常数),
(a为常数),
如图所示,根据图中提供的信息,回答下列问题:
(Ⅰ)从药物释放开始,求每立方米空气中的含药量
y(毫克)与时间t(小时)之间的函数关系式?
(Ⅱ)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那从药物释放开始,至少需要经过多少小时后,学生才能回到教室.
如图,在四棱锥 中, ,底面 是等腰梯形, , .
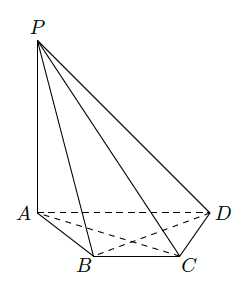
(Ⅰ)证明:
;
(Ⅱ)若
,
,直线
与平面
所成的角为30°,求四棱锥
的体积.
已知函数 的部分图像如图所示.
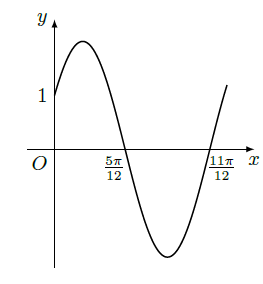
(Ⅰ)求函数
的解析式;
(Ⅱ)求函数
的单调递增区间.
某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示.
| 一次购物量 |
1至4件 |
5至8件 |
9至12件 |
13至16件 |
17件及以上 |
| 顾客数(人) |
30 |
25 |
10 |
||
| 结算时间(分钟/人) |
1 |
1.5 |
2 |
2.5 |
3 |
已知这100位顾客中的一次购物量超过8件的顾客占55%.
(Ⅰ)确定
,
的值,并估计顾客一次购物的结算时间的平均值;
(Ⅱ)求一位顾客一次购物的结算时间不超过2分钟的概率.(将频率视为概率)
设函数
,
为正整数,
为常数,曲线
在
处的切线方程为
.
(1)求
的值;
(2)求函数 的最大值;
(3)证明: .
设
是单位圆
上任意一点,
是过点
与
轴垂直的直线,
是直线
与
轴的交点,点
在直线
上,且满足
,当点
在圆上运动时,记点
的轨迹为曲线
.
(1)求曲线
的方程,判断曲线
为何种圆锥曲线,并求其焦点坐标.
(2)过原点斜率为
的直线交曲线
于
两点,其中
在第一象限,且它在
轴上的射影为点
,直线
交曲线
于另一点
,是否存在
,使得对任意的
,都有
?若存在,请说明理由。