已知棱长为a的正方体ABCD—A1B1C1D1,E为BC中点.
(1)求B到平面B1ED距离
(2)求直线DC和平面B1ED所成角的正弦值. (12分) 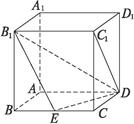
已知函数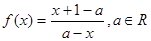 。利用函数
。利用函数 构造一个数列
构造一个数列 ,方法如下:对于定义域中给定的
,方法如下:对于定义域中给定的 ,令
,令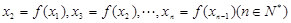 ,…
,…
如果取定义域中任一值作为 ,都可以用上述方法构造出一个无穷数列
,都可以用上述方法构造出一个无穷数列 。
。
(1)求实数a的值;
(2)若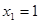 ,求
,求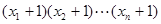 的值;
的值;
(3)设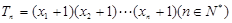 ,试问:是否存在n使得
,试问:是否存在n使得 成立,若存在,试确定n及相应的
成立,若存在,试确定n及相应的 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
已知数列{an}中,a1=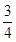 ,an+1=
,an+1= (n∈N*).
(n∈N*).
(1)求证:数列{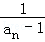 }是等差数列,并求{an}的通项公式;
}是等差数列,并求{an}的通项公式;
(2)设bn+an=l(n∈N*),S=b1b2+b2b3+…+bnbn+1,试比较an与8Sn的大小.
已知向量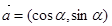 ,
, ,
,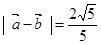 。
。
(1)求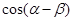 的值;
的值;
(2)若 且
且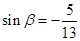 ,求
,求 的值。
的值。
在△ABC中,内角A,B,C的对边分别为a,b,c,若b=1,c= .
.
(Ⅰ)求角C的取值范围;
(Ⅱ)求4sinCcos(C )的最小值.
)的最小值.
已知函数 ,
, .
.
(Ⅰ)若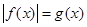 有且仅有两个不同的解,求
有且仅有两个不同的解,求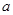 的值;
的值;
(Ⅱ)若当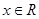 时,不等式
时,不等式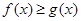 恒成立,求实数
恒成立,求实数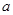 的取值范围;
的取值范围;
(Ⅲ)若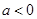 时,求
时,求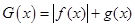 在
在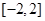 上的最大值.
上的最大值.