已知函数 R,且
R,且
(I)若 能表示成一个奇函数
能表示成一个奇函数 和一个偶函数
和一个偶函数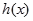 的和,求
的和,求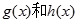 的解析式;
的解析式;
(II)命题P:函数 在区间
在区间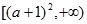 上是增函数;
上是增函数;
命题Q:函数 是减函数。
是减函数。
如果命题P、Q有且仅有一个是真命题,求a的取值范围;
(III)在(II)的条件下,比较 的大小。
的大小。
(本小题满分14分)已知函数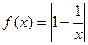 ,(x>0).
,(x>0).
(1)当0<a<b,且f(a)=f(b)时,求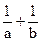 的值;
的值;
(2)是否存在实数a,b(a<b),使得函数y=f(x)的定义域、值域都是[a,b],若存在,求出a,b的值,若不存在,请说明理由.
(3) 若存在实数a,b(a<b),使得函数y=f(x)的定义域为 [a,b]时,值域为 [
若存在实数a,b(a<b),使得函数y=f(x)的定义域为 [a,b]时,值域为 [ ma,mb],(m≠0),求m的取值范围.
ma,mb],(m≠0),求m的取值范围.
(本小题满分14分)已知函数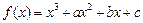 在
在 处的切
处的切 线方程为
线方程为 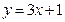 ,
,
(1)若函数 在
在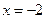 时有极值,求
时有极值,求 的表达式;
的表达式;
(2)在(1)条件下,若函数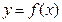 在
在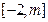 上的值域为
上的值域为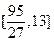 ,求m的取值范围;
,求m的取值范围;
(3)若函数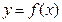 在区间
在区间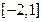 上
上 单调递增,求b的取值范围. [
单调递增,求b的取值范围. [
(本小题满分14分)已知定义域为R的函数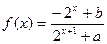 是奇函数.
是奇函数.
(1)求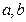 的值,并判断
的值,并判断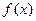 的单调性;
的单调性;
(2)若对任意 ,不等式
,不等式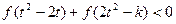 恒成立,求k的取值范围.
恒成立,求k的取值范围.
(本小题满分14分)向量 满足
满足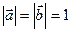 ,
,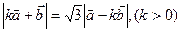 .
.
(1)求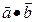 关于k的解析式
关于k的解析式 ;
;
(2)请你分别探讨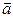 ⊥
⊥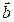 和
和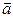 ∥
∥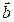 的可能性,若不可能,请说明理由,若可能,求出k的值;
的可能性,若不可能,请说明理由,若可能,求出k的值;
(3)求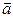 与
与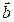 夹角的最大值.
夹角的最大值.
(本小题满分12分)某租赁公司有汽车100辆,当每辆车月租金为3000元时,可全租出,当每辆车月租金每增加50元,未租出的车将会增加 一辆.
一辆. 租出的车每辆每月需维护费150元,未租出的车每辆每月需维护费50元.
租出的车每辆每月需维护费150元,未租出的车每辆每月需维护费50元.
(1)当每辆车月租金定为3600元时,能租出多少辆车?此时的月收益是多少?
(2)每辆车的月租金定为多少元时,租赁公司的月收益最大?