(本小题满分12分)
如图,直角梯形ABCD中,∠B=90°,AD//BC,AD=1,BC=2,
∠C=60°,将该梯形绕着AB所在的直线为轴旋转一周,求该旋转体的表面积和体积。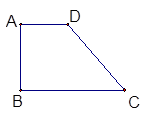
(本小题满分7分)选修4-2:矩阵与变换
已知矩阵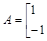
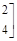 .
.
(1)求 的逆矩阵
的逆矩阵 ;
;
(2)求矩阵 的特征值
的特征值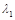 、
、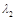 和对应的一个特征向量
和对应的一个特征向量 、
、 .
.
(本小题满分14分)已知函数 的导函数是
的导函数是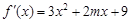 ,
, 在
在 处取得极值,且
处取得极值,且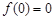 ,
,
(1)求 的极大值和极小值;
的极大值和极小值;
(2)记 在闭区间
在闭区间 上的最大值为
上的最大值为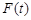 ,若对任意的
,若对任意的
 总有
总有 成立,求
成立,求 的取值范围;
的取值范围;
(Ⅲ)设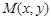 是曲线
是曲线 上的任意一点.当
上的任意一点.当 时,求直线OM斜率的最小值,据此判断
时,求直线OM斜率的最小值,据此判断 与
与 的大小关系,并说明理由.
的大小关系,并说明理由.
(本小题满分13分)某市某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域近似地为半径是R的圆面.该圆面的内接四边形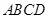 是原棚户建筑用地,测量可知边界
是原棚户建筑用地,测量可知边界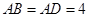 万米,
万米,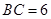 万米,
万米,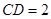 万米.
万米.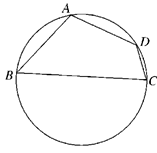
(1)请计算原棚户区建筑用地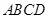 的面积及圆面的半径
的面积及圆面的半径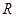 的值;
的值;
(2)因地理条件的限制,边界 、
、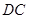 不能变更,而边界
不能变更,而边界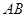 、
、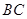 可以调整,为了提高棚户区改造建筑用地的利用率,请在圆弧
可以调整,为了提高棚户区改造建筑用地的利用率,请在圆弧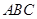 上设计一点
上设计一点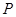 ;使得棚户区改造的新建筑用地
;使得棚户区改造的新建筑用地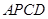 的面积最大,并求最大值.
的面积最大,并求最大值.
(本小题满分13分)若向量 其中
其中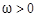 ,记函数
,记函数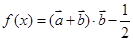 ,若函数
,若函数 的图像与直线
的图像与直线 (
( 为常数)相切,并且切点的横坐标依次成公差为
为常数)相切,并且切点的横坐标依次成公差为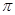 的等差数列.
的等差数列.
(1)求 的表达式及
的表达式及 的值;
的值;
(2)将函数 的图像向左平移
的图像向左平移 ,得到
,得到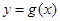 的图像,当
的图像,当 时,
时,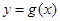 与
与 图象的交点横坐标成等比数列,求钝角
图象的交点横坐标成等比数列,求钝角 的值.
的值.
(本小题满分13分)在平面直角坐标系中,角 ,
, 的始边为
的始边为 轴的非负半轴,点
轴的非负半轴,点 在角
在角 的终边上,点
的终边上,点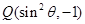 在角
在角 的终边上,且
的终边上,且 .
.
(1)求 ;
;
(2)求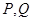 的坐标并求
的坐标并求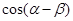 的值.
的值.