如图,已知椭圆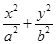 (a>b>0)的离心率
(a>b>0)的离心率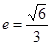 ,过点
,过点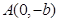 和
和 的直线与原点的距离为
的直线与原点的距离为 .
.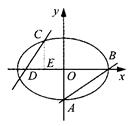
(1)求椭圆的方程;
(2)已知定点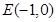 ,若直线
,若直线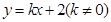 与椭圆交于
与椭圆交于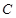 、
、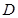 两 点.问:是否存在
两 点.问:是否存在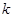 的值,
的值,
使以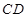 为直径的圆过
为直径的圆过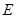 点?请说明理由.
点?请说明理由.
(本题满分12分)如图,四棱锥P—ABCD中,PA⊥ABCD,四边形ABCD 是矩形. E、F分别是AB、PD的中点.若PA=AD=3,CD= .(1)求证:AF//平面PCE;
.(1)求证:AF//平面PCE;
(2)求点A到平面PCE的距离;(3)求直线FC与平面PCE所成角的大小。
有混在一起质地均匀且粗细相同的长分别为1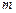 、2
、2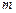 、3
、3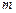 的钢管各3根(每根钢管附有不同的编号),现随意抽取4根(假设各钢管被抽取的可能性是均等的),再将抽取的4根首尾相接焊成笔直的一根.
的钢管各3根(每根钢管附有不同的编号),现随意抽取4根(假设各钢管被抽取的可能性是均等的),再将抽取的4根首尾相接焊成笔直的一根.
(1)若用ξ表示新焊成的钢管的长度(焊接误差不计),试求随机变量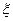 的分布列及
的分布列及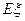 ;
;
(2)设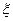 的取值从小到大依次为
的取值从小到大依次为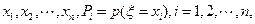 数列
数列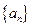 是首项为1,公差为
是首项为1,公差为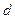 的等差数列,设
的等差数列,设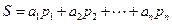 ,当
,当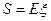 时,求
时,求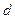 的值。
的值。
(本题满分12分)在△ABC中,三个内角是A,B,C的对边分别是a,b,c,其中c=10,且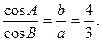 (1)求证:
(1)求证: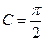 ;(2)设圆O过A,B,C三点,点P位于劣弧
;(2)设圆O过A,B,C三点,点P位于劣弧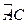 上,∠PAB=60°,求四边形ABCP的面积。
上,∠PAB=60°,求四边形ABCP的面积。
文(本小题满分12分)已知点A(-1,0),B(1,-1)和抛物线. ,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图.
,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图.
(I)若△POM的面积为 ,求向量
,求向量 与
与 的夹角。
的夹角。 (II)试证明直线PQ恒过一个定点。
(II)试证明直线PQ恒过一个定点。
(文)数列{an}中a1=0, ,(1)求证数列
,(1)求证数列 为等差数列,并求出公差;(2)设数列{an}的前n项和为Sn,证明Sn<n-ln(n+1);(3)设
为等差数列,并求出公差;(2)设数列{an}的前n项和为Sn,证明Sn<n-ln(n+1);(3)设 ,证明:对任意正整数n,m,都有
,证明:对任意正整数n,m,都有 .
.