已知椭圆 ,过点(m,0)作圆
,过点(m,0)作圆 的切线
的切线 交椭圆G于A,B两点.
交椭圆G于A,B两点.
(1)求椭圆G的焦点坐标和离心率;
(2)将 表示为m的函数,并求
表示为m的函数,并求 的最大值.
的最大值.
(本小题满分10分)已知函数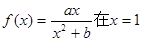 处取得极值2。
处取得极值2。
(Ⅰ)求函数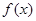 的解析式;
的解析式;
(Ⅱ)当m满足什么条件时,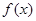 在区间
在区间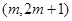 为增函数;
为增函数;
(本小题满分12分)
已知函数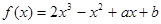
(1)若
(2)若函数 的图像上有与
的图像上有与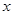 轴平行的切线,求
轴平行的切线,求 的取值范围。
的取值范围。
(3)若函数

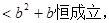 求
求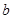 的取值范围。
的取值范围。
(本小题满分12分)
在经济学中,函数f(x)的边际函数Mf(x)定义为Mf(x)=f(x+1)-f(x).某公司每月生产x台某种产品的收入为R(x)元,成本为C(x)元,且R(x)=3 000x-20x2,C(x)=500x+4 000(x∈N*).现已知该公司每月生产该产品不超过100台.
(1)求利润函数P(x)以及它的边际利润函数MP(x);
(2)求利润函数的最大值与边际利润函数的最大值之差.
(本小题满分12分)
已知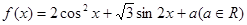
(1)若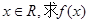 的单调递增区间;
的单调递增区间;
(2)若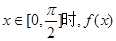 的最大值为4,求a的值;
的最大值为4,求a的值;
(本小题满分12分)
已知在△ABC中,AC=2,BC=1,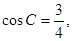
(1)求AB的值;
(2)求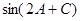 的值。
的值。