(本小题10分)
求下列函数导数
(1) f(x)=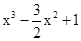 (2)
(2)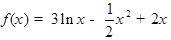
(本小题满分13分)
城市公交车的数量若太多则容易造成资源的浪费;若太少又难以满足乘客需求。某市公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间作为样本分成5组,如下表所示(单位:分钟).
| 组别 |
一 |
二 |
三 |
四 |
五 |
| 候车时间 |
[0,5) |
[5,10) |
[10,15) |
[15,20) |
[20,25] |
| 人数 |
2 |
6 |
4 |
2 |
l |
(Ⅰ)估计这60名乘客中候车时间少于10分钟的人数;
(Ⅱ)若从上表第三、四组的6人中任选2人作进一步的调查.
①列出所有可能的结果;
②求抽到的两人恰好来自不同组的概率.
(本小题满分14分)已知函数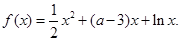
(Ⅰ)若函数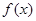 是定义域上的单调函数,求实数
是定义域上的单调函数,求实数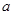 的最小值;
的最小值;
(Ⅱ)方程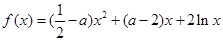 有两个不同的实数解,求实数
有两个不同的实数解,求实数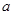 的取值范围;
的取值范围;
(Ⅲ)在函数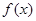 的图象上是否存在不同两点
的图象上是否存在不同两点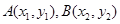 ,线段
,线段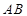 的中点的横坐标为
的中点的横坐标为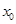 ,有
,有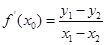 成立?若存在,请求出
成立?若存在,请求出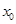 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(本小题满分14分)已知函数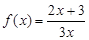 ,数列
,数列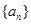 满足
满足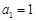 ,
,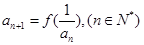 ,
,
(1)求数列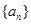 的通项公式;
的通项公式;
(2)设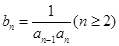 ,
,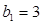 ,
,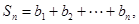 若
若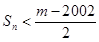 对一切
对一切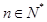 成立,求最小正整数
成立,求最小正整数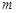 的值.
的值.
(本小题满分13分)如图,焦距为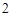 的椭圆
的椭圆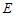 的两个顶点分别为
的两个顶点分别为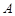 和
和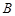 ,且
,且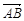 与n
与n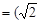 ,
,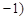 共线.
共线.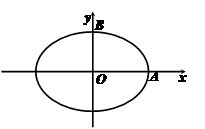
(Ⅰ)求椭圆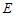 的标准方程;
的标准方程;
(Ⅱ)若直线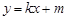 与椭圆
与椭圆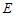 有两个不同的交点
有两个不同的交点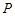 和
和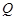 ,且原点
,且原点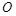 总在以
总在以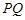 为直径的圆的内部,求实数
为直径的圆的内部,求实数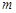 的取值范围.
的取值范围.
(本小题满分13分)如图,在四棱锥 中,底面
中,底面 是等腰梯形,
是等腰梯形,  ∥
∥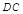 ,
, ,
,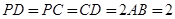 ,
,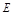 为
为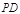 的中点.
的中点.
(Ⅰ)求证: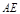 ∥平面
∥平面 ;
;
(Ⅱ)若
(ⅰ)求证平面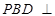 平面
平面 ;
;
(ⅱ)求直线 与底面
与底面 成角的正弦值.
成角的正弦值.