先化简,再求值: , 其中
, 其中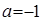 ,
,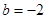 .
.
如图,在平面直角坐标系中,抛物线 与 轴交于点 、点 ,与 轴交于点 .
(1)求拋物线的解析式;
(2)过点 作直线 轴,点 在直线 上且 ,直接写出点 的坐标.
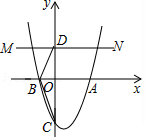
如图,在平面直角坐标系中,矩形 的边 在 轴上, 、 的长分别是一元二次方程 的两个根 , ,边 交 轴于点 ,动点 以每秒1个单位长度的速度,从点 出发沿折线段 向点 运动,运动的时间为 秒,设 的面积为 .
(1)求点 的坐标;
(2)求 关于 的函数关系式,并写出自变量的取值范围;
(3)在点 运动的过程中,是否存在点 ,使 是以 为腰的等腰三角形?若存在,直接写出点 的坐标;若不存在,请说明理由.

为庆祝中华人民共和国七十周年华诞,某广场舞团队准备购买甲、乙两种道具参加演出,已知购买2件甲种道具、1件乙种道具共需35元;购买1件甲种道具、3种乙种道具共需花费30元.
(1)求购买一件甲种道具,一件乙种道具各需多少元?
(2)若该团体计划购买这两种道具共120件,投入资金不少于956元又不多于1000元,设购买甲种道具 件,求有多少种购买方案?
(3)设投入资金为 元,在(2)的条件下,哪种购买方案需要投入的资金最少?最少资金是多少元?
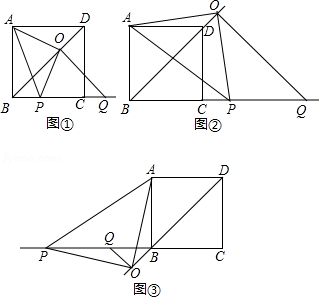
如图, 是正方形 的对角线,线段 在其所在的直线上平移,将平移得到的线段记为 ,连接 ,过点 作 ,垂足为 ,连接 、 .
(1)如图①所示,求证: ;
(2)如图②所示, 在 的延长线上,如图③所示, 在 的反向延长线上,猜想线段 、 之间有怎样的数量关系?请直接写出你的猜想,不需证明.
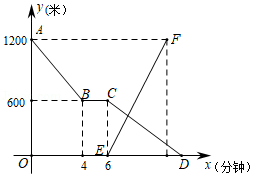
小明匀速跑步从甲地到乙地,在途中因故停留了一段时间后,仍按原速跑步,小强骑自行车比小明晚出发一段时间,以400米 分的速度匀速从乙地到甲地,两人距离乙地的路程 (米 与小明出发后所用时间 (分钟)之间的函数图象如图所示,
(1)求小明跑步的速度;
(2)求小明停留结束后 与 之间的函数解析式,并写出自变量的取值范围;
(3)求小明与小强相遇时 的值.