如图,如果∠1=∠2,那么∠2+∠3=1800吗?为什么?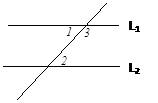
如图是一个转盘,(转盘被等分成四个扇形),上面标有红黄蓝三种颜色.小明和小强做游戏,规定:转到红色,小明赢;转到黄色,小强赢(若转到分界线,再重转一次).
(1)小颖认为转盘上共有三种不同的颜色,所以,指针停在红色、黄色或蓝色区域的概率都是 ,他们的游戏对小明和小强都是公平的.你认为呢?请说明理由.
,他们的游戏对小明和小强都是公平的.你认为呢?请说明理由.
(2)若你认为游戏不公平,请你设计一种方案,使他们的游戏公平.
如图,△ABC中,∠ABC与∠ACB的平分线相交于F,过F作DE∥BC交AB于D,交AC于E,若BD+CE=9,求线段DE的长.
如图,在B港有甲乙两艘渔船,若甲船沿北偏东50方向以每小时8海里的速度前进,乙船沿南偏东某方向以每小时15 海里的速度前行,1小时后,甲船到M岛,乙船到P岛,两岛相距17海里,你能知道乙船沿哪个方向航行吗?
阅读下面的文字,解答问题.
大家知道 是无理数,由于1<
是无理数,由于1< <2,因此
<2,因此 的整数部分为1,将
的整数部分为1,将 减去其整数部分1,差就是小数部分
减去其整数部分1,差就是小数部分 -1.请解答:
-1.请解答:
(1) 的整数部分是,小数部分是.
的整数部分是,小数部分是.
(2) 2+ 的整数部分为x,小数部分为y,求x-y.
的整数部分为x,小数部分为y,求x-y.
(本题满分6分,每小题2分) 掷一枚骰子,观察向上一面的点数,则下列事件的概率分别为:
(1)点数为3的概率为.
(2)点数为偶数的概率为.
(3)点数大于2且小于5的概率为.