(本小题满分15分)、某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成.已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米.
(1)若设休闲区的长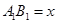 米,求公园ABCD所占面积S关于
米,求公园ABCD所占面积S关于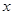 的函数
的函数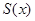 的解析式;
的解析式;
(2)要使公园所占面积最小,休闲区A1B1C1D1的长和宽该如何设计?
(本题满分16分,第(1)小题4分,第(2)小题6分,第(2)小题6分)
设数列 中,若
中,若 ,则称数列
,则称数列 为“凸数列”。
为“凸数列”。
(1)设数列 为“凸数列”,若
为“凸数列”,若 ,试写出该数列的前6项,并求出该6项之和;
,试写出该数列的前6项,并求出该6项之和;
(2)在“凸数列” 中,求证:
中,求证: ;
;
(3)设 ,若数列
,若数列 为“凸数列”,求数列前2010项和
为“凸数列”,求数列前2010项和 。
。
(本题满分14分,第(1)小题6分,第(2)小题8分)
设 分别为
分别为 的内角
的内角 的对边,
的对边,
 与
与 的夹角为
的夹角为
(1)求角 的大小;
的大小;
(2)已知 ,
, 的面积
的面积 ,求
,求 的值。
的值。
(本题满分14分,第(1)小题6分,第(2)小题8分)
设函数 ,若不等式
,若不等式 的解集为
的解集为 。
。 (1)求
(1)求 的值;
的值;
(2)若函数 在
在 上的最小值为1,求实数
上的最小值为1,求实数 的值。
的值。
(本题满分18分,第(1)小题4分,第(2)小题6分,第(3)小题8分)
在平行四边形 中,已知过点
中,已知过点 的直线与线段
的直线与线段 分别相交于点
分别相交于点 。若
。若 。
。
(1)求证: 与
与 的关系为
的关系为 ;
;
(2)设 ,定义函数
,定义函数 ,点列
,点列 在函数
在函数 的图像上,且数列
的图像上,且数列 是以首项为1,公比为
是以首项为1,公比为 的等比数列,
的等比数列, 为原点,令
为原点,令 ,是否存在点
,是否存在点
 ,使得
,使得 ?若存在,请求出
?若存在,请求出 点坐标;若不存在,请说明理由。
点坐标;若不存在,请说明理由。
(3)设函数 为
为 上偶函数,当
上偶函数,当 时
时 ,又函数
,又函数 图象关于直线
图象关于直线 对称,当方程
对称,当方程 在
在 上有两个不同的实数解时,求实数
上有两个不同的实数解时,求实数 的取值范围。
的取值范围。
(本题满分16分,第(1)小题4分,第(2)小题8分,第(3)小题4分)
已知椭圆 的左右焦点分别为
的左右焦点分别为 ,短轴两个端点为
,短轴两个端点为 ,且四边形
,且四边形 是边长为2的正方形。
是边长为2的正方形。
(1)求椭圆方程;
(2)若 分别是椭圆长轴的左右端点,动点
分别是椭圆长轴的左右端点,动点 满足
满足 ,连接
,连接 ,交椭圆于
,交椭圆于 点
点 。证明:
。证明: 为定值;
为定值;
(3)在(2)的条件下,试问 轴上是否存在异于点
轴上是否存在异于点 的定点
的定点 ,使得以
,使得以 为直径的圆恒过直线
为直径的圆恒过直线 的交点,若存在,求出点
的交点,若存在,求出点 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。