如图,在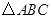 中,
中, ,点
,点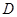 在
在 边上,且
边上,且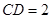 ,
, .
.
(1)求 ;
;
(2)求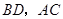 的长.
的长.
(本小题满分1 2分)
2分)
设锐角三角形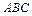 的内角
的内角 的对边分别为
的对边分别为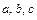 ,且
,且 .
.
(Ⅰ)求 的大小;
的大小;
(Ⅱ)求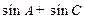 的取值范围.
的取值范围.
(本小题满分10分)选修4—5:不等式选讲
已知函数 ,
,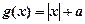
(Ⅰ)当 时,解不等式
时,解不等式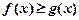 ;
;
(Ⅱ)若存在 ,使得
,使得 成立,求实数
成立,求实数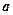 的取值范围.
的取值范围.
(本小题满分10分)选修4—4:坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系的x轴的正半轴重合.设点O为坐标原点, 直线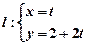 (参数
(参数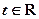 )与曲线
)与曲线 的极坐标方程为
的极坐标方程为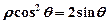
(Ⅰ)求直线l与曲线C的普通方程;
(Ⅱ)设直线l与曲线C相交于A,B两点,证明: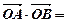 0.
0.
请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.
(本小题满分10分)选修4—1:几何证明选讲
如图,AB是⊙O的直径,弦BD、CA的延长线相交于
点E,EF垂直B A的延长线于点F. 求证:
A的延长线于点F. 求证:
(Ⅰ)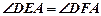 ;
;
(Ⅱ)

(本小题满分12分)
已知函数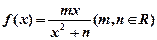 在
在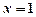 处取到极值2
处取到极值2
(Ⅰ)求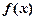 的解析式;
的解析式;
(Ⅱ)设函数 .若对任意的
.若对任意的 ,总存在唯一的
,总存在唯一的 ,使得
,使得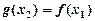 ,求实数
,求实数 的取值范围.
的取值范围.