已知抛物线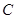 :
: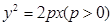 过点
过点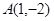 .(1)求抛物线
.(1)求抛物线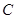 的方程,并求其准线方程;
的方程,并求其准线方程;
(2)是否存在平行于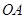 (
(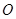 为坐标原点)的直线
为坐标原点)的直线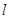 ,使得直线
,使得直线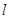 与抛物线
与抛物线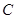 有公共点,且直线
有公共点,且直线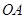 与
与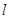 的
的
距离等于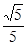 ?若存在,求出直线
?若存在,求出直线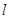 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
已知函数 。
。
(Ⅰ)设 ,讨论
,讨论 的单调性;
的单调性;
(Ⅱ)若对任意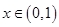 恒有
恒有 ,求
,求 的取值范围。
的取值范围。
已知  是等差数列,
是等差数列,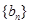 是公比为
是公比为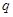 的等比数列,
的等比数列,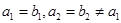 ,记
,记 为数列
为数列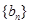 的前
的前 项和,
项和,
(1)若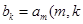 是大于
是大于 的正整数
的正整数 ,求证:
,求证: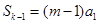 ;
;
(2)若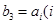 是某一正整数
是某一正整数 ,求证:
,求证: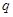 是整数,且数列
是整数,且数列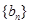 中每一项都是数列
中每一项都是数列 中的项;
中的项;
(3)是否存在这样的正数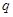 ,使等比数列
,使等比数列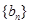 中有三项成等差数列?若存在,写出一个
中有三项成等差数列?若存在,写出一个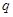 的值,并加以说明;若不存在,请说明理由;
的值,并加以说明;若不存在,请说明理由;
已知椭圆C1: ,抛物线C2:
,抛物线C2: ,且C1、C2的公共弦AB过椭圆C1的右焦点.
,且C1、C2的公共弦AB过椭圆C1的右焦点.
(Ⅰ)当AB⊥ 轴时,求
轴时,求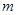 、
、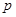 的值,并判断抛物线C2的焦点是否在直线AB上;
的值,并判断抛物线C2的焦点是否在直线AB上;
(Ⅱ)是否存在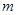 、
、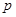 的值,使抛物线C2的焦点恰在直线AB上?若存在,求出符合条件的
的值,使抛物线C2的焦点恰在直线AB上?若存在,求出符合条件的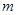 、
、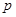 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知两个正四棱锥P-ABCD与Q-ABCD的高分别为1和2,AB=4.
(Ⅰ)证明PQ⊥平面ABCD;
(Ⅱ)求异面直线AQ与PB所成的角;
(Ⅲ)求点P到平面QAD的距离.
A、B是治疗同一种疾病的两种药,用若干试验组进行对比试验。每个试验组由4只小白鼠组成,其中2只服用A,另2只服用B,然后观察疗效。若在一个试验组中,服用A有效的小白鼠的只数比服用B有效的多,就称该试验组为甲类组。设每只小白鼠服用A有效的概率为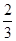 ,服用B有效的概率为
,服用B有效的概率为 。
。
(Ⅰ)求一个试验组为甲类组的概率;
(Ⅱ)观察3个试验组,用 表示这3个试验组中甲类组的个数,求
表示这3个试验组中甲类组的个数,求 的分布列和数学期望。
的分布列和数学期望。