如图,已知在直四棱柱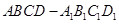 中,
中,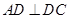 ,
, ,
,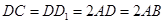
 .
.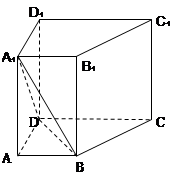
(1)求证: 平面
平面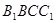 ;
;
(2)设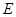 是
是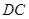 上一点,试确定
上一点,试确定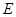 的位置,使
的位置,使 平面
平面 ,并说明理由.
,并说明理由.
设函数f(x)="|x-1|" +|x-a|, .
.
(I)当a =4时,求不等式 的解集;
的解集;
(II)若 对
对 恒成立,求a的取值范围.
恒成立,求a的取值范围.
以直角坐标系的原点O为极点,x轴正半轴为极轴,并在两种坐标系中取相同的长度单位.已知直线I的参数方程为 (t为参数,O < a <
(t为参数,O < a < ),曲线C的极坐标方程为
),曲线C的极坐标方程为
(I)求曲线C的直角坐标方程;
(II)设直线l与曲线C相交于A ,B两点,当a变化时,求 的最小值.
的最小值.
如图所示,PA为 0的切线,A为切点,PBC是过点O的割线,PA ="10,PB" =5、
0的切线,A为切点,PBC是过点O的割线,PA ="10,PB" =5、
(I)求证: ;
;
(2)求AC的值.
已知函数 在点(1,f(1))处的切线方程为y = 2.
在点(1,f(1))处的切线方程为y = 2.
(I)求f(x)的解析式;
(II)设函数 若对任意的
若对任意的 ,总存唯一实数
,总存唯一实数 ,使得
,使得 ,求实数a的取值范围.
,求实数a的取值范围.
已知椭圆C:  (a>b>0)的两个焦点和短轴的两个端点都在圆
(a>b>0)的两个焦点和短轴的两个端点都在圆 上.
上.
(I)求椭圆C的方程;
(II)若斜率为k的直线过点M(2,0),且与椭圆C相交于A, B两点.试探讨k为何值时,三角形OAB为直角三角形.