(本小题满分13分)
已知直线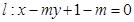
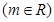 ,圆
,圆 .
.
(Ⅰ)证明:对任意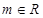 ,直线
,直线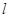 恒过一定点N,且直线
恒过一定点N,且直线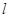 与圆C恒有两个公共点;
与圆C恒有两个公共点;
(Ⅱ)设以CN为直径的圆为圆D(D为CN中点),求证圆D的方程为: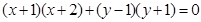
(Ⅲ)设直线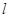 与圆
与圆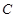 的交于A、B两点,与圆D:
的交于A、B两点,与圆D: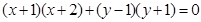 交于点
交于点 (异于C、N),当
(异于C、N),当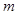 变化时,求证
变化时,求证 为AB的中点.
为AB的中点.
二次函数 满足条件:
满足条件:
①当 时,
时,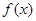 的图象关于直线
的图象关于直线 对称;
对称;
② 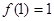 ;
;
③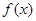 在
在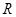 上的最小值为
上的最小值为 ;
;
(1)求函数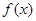 的解析式;
的解析式;
(2)求最大的 ,使得存在
,使得存在 ,只要
,只要 ,就有
,就有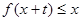 .
.
已知函数
(1)求函数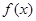 的最小值;
的最小值;
(2)求实数 的取值范围,使
的取值范围,使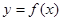 在区间
在区间 上是单调函数.
上是单调函数.
已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8、高为4的等腰三角形,侧视图是一个底边长为6、高为4的等腰三角形.
(1)求该几何体的体积V;(2)求该几何体的侧面积S。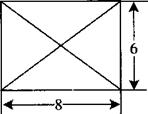
、(本小题满分13分).在正方体ABCD-A1B1C1D1中,M、N、P分别是CC1、B1C1、C1D1的中点.(温馨提示:该题要在答题卡上作图,否则扣分)。
(1) 求异面直线PN、AC所成角; (2) 求证:平面MNP∥平面A1BD.
定义在R上的函数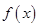 满足:对任意实数
满足:对任意实数 ,总有
,总有 ,且当
,且当 时,
时, .
.
(1)试求 的值;
的值;
(2)判断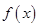 的单调性并证明你的结论;
的单调性并证明你的结论;