已知梯形ABCD中，AD∥BC，∠ABC ="∠BAD" =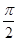
，AB=BC=2AD=4，
E、F分别是AB、CD上的点，且EF∥BC.设AE =
，G是BC的中点．
沿EF将梯形ABCD翻折，使平面AEFD⊥平面EBCF （如图）．
（1）当=2时，求证：BD⊥EG ；
（2）若以F、B、C、D为顶点的三棱锥的体积记为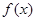
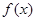，求的最大值；
（3）当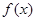取得最大值时，求二面角D-BF-E的余弦值．
（本小题满分13分）
已知椭圆E的中心在坐标原点，焦点在x轴上，离心率为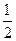
，且椭圆E上一点到两个焦点距离之和为4；
是过点P（0，2）且互相垂直的两条直线，
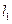交E于A，B两点，
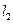交E交C，D两点，AB，CD的中点分别为M，N。
（1）求椭圆E的方程；
（2）求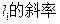
k的取值范围；
（3）求
的取值范围。
（本小题满分13分）
在数列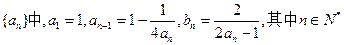
。
（1）求证：数列
是等差数列，并求数列
的通项公式
；
（2）设
，求数列
的前
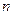项和。
（本小题满分12分）
在如图所示的空间几何体中，平面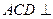
平面ABC，AB=BC=CA=DA=DC=BE=2，BE和平面ABC所成的角为60°，且点E在平面ABC上的射影落在
的平分线上。
（1）求证：DE//平面ABC；
（2）求二面角E—BC—A的余弦；
（3）求多面体ABCDE的体积。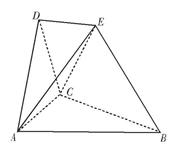
（本小题满分12分）
甲乙两个盒子里各放有标号为1，2，3，4的四个大小形状完全相同的小球，从甲盒中任取一小球，记下号码
后放入乙盒，再从乙盒中任取一小球，记下号码
，设随机变量
（1）求
的概率；
（2）求随机变量X的分布列及数学期望。
（本小题满分12分）
在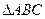
，角A，B，C的对边分别为
。
（1）判断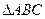的形状；
（2）若
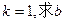的值。