已知椭圆 ,
, 为坐标原点,椭圆的右准线与
为坐标原点,椭圆的右准线与 轴的交点是
轴的交点是 .
.
(1)点 在已知椭圆上,动点
在已知椭圆上,动点 满足
满足 ,求动点
,求动点 的轨迹方程;
的轨迹方程;
(2)过椭圆右焦点 的直线与椭圆交于点
的直线与椭圆交于点 ,求
,求 的面积的最大值
的面积的最大值
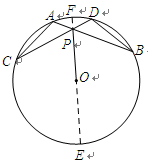
如图,⊙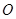 的半径为3,两条弦
的半径为3,两条弦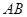 ,
,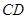 交于点
交于点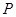 ,且
,且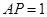 ,
, 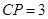 ,
,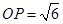 .
.
求证:△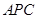 ≌△
≌△ .
.
设 是定义在
是定义在 的可导函数,且不恒为0,记
的可导函数,且不恒为0,记 .若对定义域内的每一个
.若对定义域内的每一个 ,总有
,总有 ,则称
,则称 为“
为“ 阶负函数 ”;若对定义域内的每一个
阶负函数 ”;若对定义域内的每一个 ,总有
,总有 ,则称
,则称 为“
为“ 阶不减函数”(
阶不减函数”( 为函数
为函数 的导函数).
的导函数).
(1)若 既是“1阶负函数”,又是“1阶不减函数”,求实数
既是“1阶负函数”,又是“1阶不减函数”,求实数 的取值范围;
的取值范围;
(2)对任给的“2阶不减函数” ,如果存在常数
,如果存在常数 ,使得
,使得 恒成立,试判断
恒成立,试判断 是否为“2阶负函数”?并说明理由.
是否为“2阶负函数”?并说明理由.
已知数列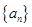 是首项为1,公差为
是首项为1,公差为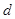 的等差数列,数列
的等差数列,数列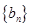 是首项为1,公比为
是首项为1,公比为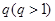 的等比数列.
的等比数列.
(1)若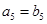 ,
,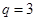 ,求数列
,求数列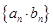 的前
的前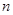 项和;
项和;
(2)若存在正整数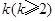 ,使得
,使得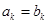 .试比较
.试比较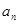 与
与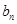 的大小,并说明理由.
的大小,并说明理由.
如图,在平面直角坐标系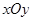 中,椭圆
中,椭圆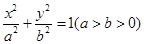 的右焦点为
的右焦点为 ,离心率为
,离心率为 .分别过
.分别过 ,
,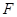 的两条弦
的两条弦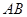 ,
, 相交于点
相交于点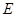 (异于
(异于 ,
, 两点),且
两点),且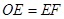 .
.
(1)求椭圆的方程;
(2)求证:直线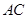 ,
, 的斜率之和为定值.
的斜率之和为定值.
某单位设计的两种密封玻璃窗如图所示:图1是单层玻璃,厚度为8 mm;图2是双层中空玻璃,厚度均为4 mm,中间留有厚度为 的空气隔层.根据热传导知识,对于厚度为
的空气隔层.根据热传导知识,对于厚度为 的均匀介质,两侧的温度差为
的均匀介质,两侧的温度差为 ,单位时间内,在单位面积上通过的热量
,单位时间内,在单位面积上通过的热量 ,其中
,其中 为热传导系数.假定单位时间内,在单位面积上通过每一层玻璃及空气隔层的热量相等.(注:玻璃的热传导系数为
为热传导系数.假定单位时间内,在单位面积上通过每一层玻璃及空气隔层的热量相等.(注:玻璃的热传导系数为 ,空气的热传导系数为
,空气的热传导系数为 .)
.)
(1)设室内,室外温度均分别为 ,
, ,内层玻璃外侧温度为
,内层玻璃外侧温度为 ,外层玻璃内侧温度为
,外层玻璃内侧温度为 ,且
,且 .试分别求出单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量(结果用
.试分别求出单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量(结果用 ,
, 及
及 表示);
表示);
(2)为使双层中空玻璃单位时间内,在单位面积上通过的热量只有单层玻璃的4%,应如何设计 的大小?
的大小?