2013年全国第十二届全运会由沈阳承办。城建部门计划在浑南新区建造一个长方形公园ABCD，公园由长方形的休闲区A1B1C1D1（阴影部分）和环公园人行道组成。已知休闲区A1B1C1D1的面积为4000平方米，人行道的宽分别为4米和10米。
（1）若设休闲区的长
米，求公园ABCD所占面积S关于
的函数
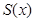的解析式；
（2）要使公园所占面积最小，休闲区A1B1C1D1的长和宽该如何设计？
（本小题满分13分）已知函数
,其中
为常数,且
．
（Ⅰ）若曲线
在点（1，
）处的切线与直线
垂直，求的值；
（Ⅱ）若函数
在区间[1，2]上的最小值的表达式．
（本小题满分13分）从含有两件正品和一件次品的3件产品中，每次任取1件
（Ⅰ）每次取出后不放回，连续取两次，求取出的产品中恰有一件次品的概率；
（Ⅱ）每次取出后放回，连续取两次，求取出的产品中恰有一件次品的概率．
（本小题满分14分） 如图，在四棱锥
中，底面
为矩形，平面
平面
，
，
，
为
的中点，求证：
（Ⅰ）
平面
；
（Ⅱ）平面
平面
；
（Ⅲ）求四棱锥的体积．
（本小题满分13分）已知函数
，
（Ⅰ）求函数
的最小正周期；
（Ⅱ）记
的内角A,B,C的对边长分别为
，若
，求
的值．
（本小题共13分）将
这
个数随机排成一列，得到的一列数
称为的一个排列．定义
为排列的波动强度．
（Ⅰ）当
时，写出排列
的所有可能情况及所对应的波动强度；
（Ⅱ）当
时，求
的最大值，并指出所对应的一个排列．
（Ⅲ）当时，在一个排列中交换相邻两数的位置称为一次调整，若要求每次调整时波动强度不增加，问对任意排列
，是否一定可以经过有限次调整使其波动强度降为9；若可以，给出调整方案，若不可以，请给出一个反例并加以说明．