对于任意自然数,试说明代数式n(n+7)-(n-3)(n-2)的值都能被6整除.
如图1,已知有一张三角形纸片ABC的一边AB=10,若D为AB边上的点,过点D作DE//BC交AC于点E,分别过点D、E作DF⊥BC,EG⊥BC,垂足分别为点F、点G,把三角形纸片ABC分别沿DE、DF、EG按图1方式折叠,点A、B、C分别落在A´、B´、C´处.若A´、B´、C´在矩形DFGE内或者其边上,且互不重合,此时我们称△A´B´C´(即图中阴影部分)为“重叠三角形”.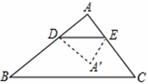
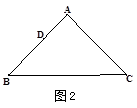
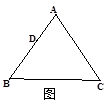
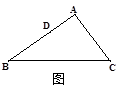

(1)实验操作:当AD=4时,①若∠A=90°,AB=AC,请在图2中画出“重叠三角形”,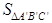 = ;
= ;
②若AB=AC,BC=12,如图3,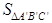 = ;③若∠B=30°,∠C=45°,如图4,
= ;③若∠B=30°,∠C=45°,如图4, = ;
= ;
(2)实验探究:若△ABC为等边三角形(如图5),设AD的长为m,若重叠三角形A´B´C´存在,试用含m的代数式表示重叠三角形A´B´C´的面积,并写出m的取值范围.
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BBl∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连结DG.设点D运动的时间为t秒.
(1)当t为何值时,AD=AB,并求出此时DE的长度;
(2)当△DEG与△ACB相似时,求t的值;
(3)以DH所在直线为对称轴,线段AC经轴对称变换后的图形为A′C′.当t>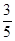 时,连结C ′C,则以CC´为直径的圆何时与直线AB相切?
时,连结C ′C,则以CC´为直径的圆何时与直线AB相切?
如图,抛物线 与直线AB交于点A(-1,0),B(4,
与直线AB交于点A(-1,0),B(4,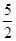 ).点D是抛物线A,B两点间部分上的一个动点(不与点A,B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.
).点D是抛物线A,B两点间部分上的一个动点(不与点A,B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.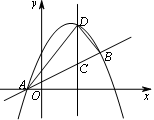
(1)求抛物线的解析式;
(2)设点D的横坐标为m,则用m的代数式表示线段DC的长;
(3)在(2)的条件下,若△ADB的面积为S,求S关于m的函数关系式,并求出当S取最大值时的点C的坐标;
(4)当点D为抛物线的顶点时,若点P是抛物线上的动点,点Q是直线AB上的动点,判断有几个位置能使以点P,Q,C,D为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
由于受到手机更新换代的影响,某手机店经销的甲品牌手机二月售价比一月每部降价500元.如果卖出相同数量的甲品牌手机,那么一月销售额为4.5万元,二月销售额只有4万元.
(1)一月甲品牌手机每部售价为多少元?
(2)为了提高利润,该店计划三月购进乙品牌手机销售,已知甲品牌每部进价为3500元,乙品牌每部进价为4000元,预计用不多于7.5万元且不少于7.4万元的资金购进这两种手机共20部,请问有哪几种进货方案?
(3)该店三月营销计划为:在二月售价基础上每售出一部甲品牌手机再返还顾客话费a元,而乙品牌按每部4400元销售,如果要使(2)中所有进货方案获利都相同,a应取何值?
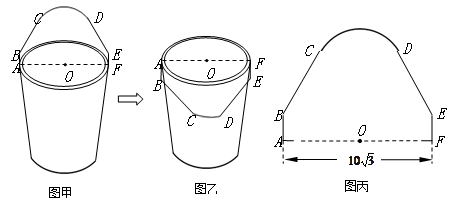
如图,图甲是一个水桶模型示意图,水桶提手结构的平面图是轴对称图形.当点O到BC(或DE)的距离大于或等于⊙O的半径时(⊙O是桶口所在圆,半径为OA),提手才能从图甲的位置转到图乙的位置,这样的提手才合格.现用金属材料做了一个水桶提手ABCDEF(如图丙,其中CD是弧,其余是线段),O是AF的中点,桶口直径AF =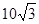 cm,AB=FE=5cm,∠ABC ="∠FED" =130°.请通过计算判断这个水桶提手是否合格.(参考数据:
cm,AB=FE=5cm,∠ABC ="∠FED" =130°.请通过计算判断这个水桶提手是否合格.(参考数据: ≈1.73,sin70°≈0.94,cos70°≈0.34,tan70°≈2.75.)
≈1.73,sin70°≈0.94,cos70°≈0.34,tan70°≈2.75.)
|