已知椭圆C: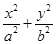 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为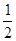 ,以原点为圆点,椭圆的短半轴为半径的圆与直线x-y+
,以原点为圆点,椭圆的短半轴为半径的圆与直线x-y+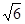 =0相切。
=0相切。
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设P(4,0),A,B是椭圆C上关于x轴对称的任意两个不同的点,连接PB交随圆C于另一点E,证明直线AE与x轴相交于定点Q.
已知命题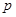 :方程
:方程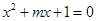 有两个不等的负实根;命题
有两个不等的负实根;命题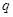 :方程
:方程 无实根, 若“
无实根, 若“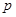 或
或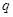 ”为真,而“
”为真,而“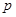 且
且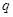 ”为假,求实数
”为假,求实数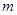 的取值范围.
的取值范围.
如图,在直三棱柱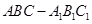 中,
中,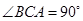 ,
,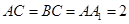 ,
,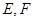 分别是
分别是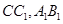 的中点。
的中点。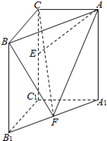
(1)求证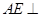 平面
平面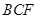 ;
;
(2)求点F到平面ABE的距离。
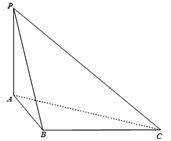
如图,三棱锥P-ABC中,PA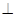 平面ABC,
平面ABC,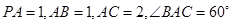 .
.
(Ⅰ)求三棱锥P-ABC的体积;
(Ⅱ)证明:在线段PC上存在点M,使得AC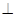 BM,并求
BM,并求 的值.
的值.
如图1,在直角梯形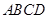 中,
中,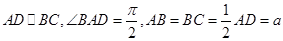 ,
,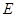 是
是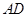 的中点,
的中点, 是AC与
是AC与 的交点,将
的交点,将 沿
沿 折起到图2中
折起到图2中 的位置,得到四棱锥
的位置,得到四棱锥 .
.

(Ⅰ)证明: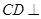 平面
平面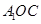 ;
;
(Ⅱ)当平面 平面
平面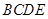 时,四棱锥
时,四棱锥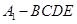 的体积为
的体积为 ,求
,求 的值.
的值.
如图,PA⊥平面ABCD,矩形ABCD的边长AB=1,BC=2,E为BC的中点.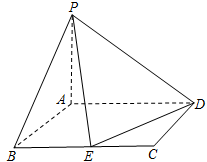
(1)证明:PE⊥DE;
(2)如果PA=2,求异面直线AE与PD所成的角的大小.