设椭圆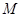 :
: 的离心率为
的离心率为 ,点
,点 (
( ,0),
,0), (0,
(0, ),原点
),原点 到直线
到直线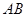 的距离为
的距离为
(Ⅰ)求椭圆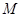 的方程;
的方程;
(Ⅱ)设点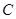 为(
为( ,0),点
,0),点 在椭圆
在椭圆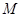 上(与
上(与 、
、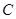 均不重合),点
均不重合),点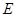 在直线
在直线 上,若直线
上,若直线 的方程为
的方程为 ,且
,且 ,试求直线
,试求直线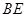 的方程.
的方程.
已知数列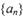 的前n项和
的前n项和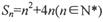 ,数列
,数列 满足b1=1,
满足b1=1,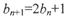
(1) 求数列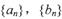 的通项公式;
的通项公式;
(2) 设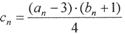 ,求数列
,求数列 的前n项和
的前n项和
已知圆的半径为1,圆心C在直线 上,其坐标为整数,圆C截直线
上,其坐标为整数,圆C截直线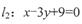 所得的弦长为
所得的弦长为
(1) 求圆C的标准方程;
(2) 设动点P在直线 上,过点P作圆的两条切线PA,PB切点分别为A,B,求四边形PACB面积的最小值.
上,过点P作圆的两条切线PA,PB切点分别为A,B,求四边形PACB面积的最小值.
已知函数 的反函数为
的反函数为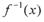 ,且
,且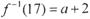
(1)求a的值;
(2)若 ,
, 是数列
是数列 的前n项和,若不等式
的前n项和,若不等式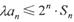 对任意
对任意 恒成立,求实数
恒成立,求实数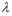 的最大值.
的最大值.
已知向量
 ,函数
,函数 —且最小正周斯为
—且最小正周斯为 ,
,
(1) 求函数,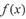 的最犬值,并写出相应的x的取值集合;
的最犬值,并写出相应的x的取值集合;
( 2)在
2)在 中角A,B,C所对的边分别为a,b,c且
中角A,B,C所对的边分别为a,b,c且 ,求b的值.
,求b的值.
已知函数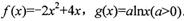
(I)若直线l1交函数f(x)的图象于P,Q两点,与l1平行的直线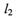 与函数
与函数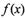 的图象切于点R,求证 P,R,Q三点的横坐标成等差数列;
的图象切于点R,求证 P,R,Q三点的横坐标成等差数列;
(II)若不等式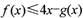 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(III)求证: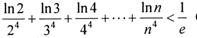 〔其中
〔其中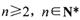 , e为自然对数的底数)
, e为自然对数的底数)