已知向量
 ,函数
,函数 —且最小正周斯为
—且最小正周斯为 ,
,
(1) 求函数,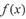 的最犬值,并写出相应的x的取值集合;
的最犬值,并写出相应的x的取值集合;
( 2)在
2)在 中角A,B,C所对的边分别为a,b,c且
中角A,B,C所对的边分别为a,b,c且 ,求b的值.
,求b的值.
(本小题满分12分)已知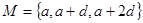 ,
, ,
,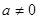 ,M=N,求q的值
,M=N,求q的值
(本小题满分12分)定义A⊗B={z|z=xy+ ,x∈A,y∈B}.设集合A={0,2},B={1,2}
,x∈A,y∈B}.设集合A={0,2},B={1,2}
1.求集合A⊗B的所有元素之和. 2.写出集合A⊗B的所有真子集。
已知函数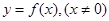 对于任意的
对于任意的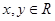 且
且 满足
满足 .
.
(1)求 的值;
的值;
(2)判断函数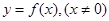 的奇偶性;
的奇偶性;
(3)若函数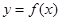 在
在 上是增函数,解不等式
上是增函数,解不等式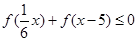 .
.
如图,已知底角为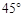 的等腰梯形
的等腰梯形 ,底边
,底边 长为
长为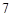 cm,腰长为
cm,腰长为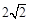 cm,当一条垂直于底边
cm,当一条垂直于底边 (垂足为
(垂足为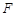 )的直线
)的直线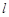 从左至右移动(与梯形
从左至右移动(与梯形 有公共点)时,直线
有公共点)时,直线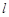 把梯形分成两部分,令
把梯形分成两部分,令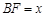 .
.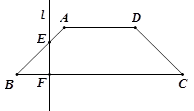
(1)求左边部分的面积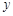 关于
关于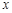 的函数解析式
的函数解析式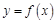 ;
;
(2)作出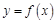 的图象.
的图象.
已知函数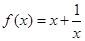
(1)判断函数的奇偶性,并加以证明;
(2)用定义证明 在
在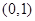 上是减函数;
上是减函数;
(3)函数 在
在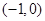 上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).