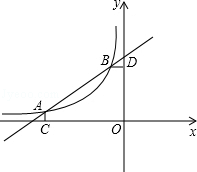
如图，已知
，
是一次函数
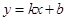的图象和反比例函数
的图象的两个交点．
(1)求反比例函数和一次函数的解析式；
(2)求直线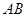
与
轴的交点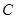
的坐标及△
的面积；
(3)求不等式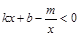
的解集（请直接写出答案）.
关于体育选考项目统计图
| 项目 |
频数 |
频率 |
| A |
80 |
b |
| B |
c |
0．3 |
| C |
20 |
0．1 |
| D |
40 |
0．2 |
| 合计 |
a |
1 |
（1）求出表中a，b，c的值，并将条形统计图补充完整．
表中a=，b=，c=．
（2）如果有3万人参加体育选考，会有多少人选择篮球？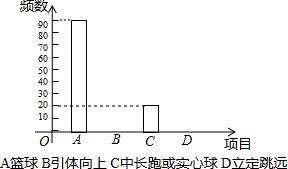
先化简，再求值：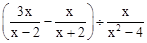
，在﹣2，0，1，2四个数中选一个合适的代入求值．
如图，在△ABC中，AB=AC，AD⊥AB点D，BC=10cm，AD=8cm，点P从点B出发，在线段BC上以每秒3cm的速度向点C匀速运动，与此同时，垂直于AD的直线m从底边BC出发，以每秒2cm的速度沿DA方向匀速平移，分别交AB、AC、AD于E、F、H，当点P到达点C时，点P与直线m同时停止运动，设运动时间为t秒（t＞0）。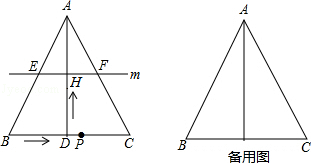
（1）当t=2时，连接DE、DF，求证：四边形AEDF为菱形；
（2）在整个运动过程中，所形成的△PEF的面积存在最大值，当△PEF的面积最大时，求线段BP的长；
（3）是否存在某一时刻t，使△PEF为直角三角形？若存在，请求出此时刻t的值，若不存在，请说明理由。
如图，⊙
是△ABC的外接圆，AC是直径，过点O作OD⊥AB于点D，延长DO交⊙于点P，过点P作PE⊥AC于点E，作射线DE交BC的延长线于F点，连接PF。
（1）若∠POC=60°，AC=12，求劣弧PC的长；（结果保留π）
（2）求证：OD=OE；
（3）求证：PF是⊙的切线。
如图，已知A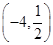
，B（-1,2）是一次函数
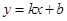与反比例函数
（
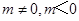）图象的两个交点，AC⊥x轴于C，BD⊥y轴于D。
(1)根据图象直接回答：在第二象限内，当x取何值时，一次函数大于反比例函数的值?
(2)求一次函数解析式及m的值；
(3)P是线段AB上的一点，连接PC，PD，若△PCA和△PDB面积相等，求点P坐标。