某批发商以每件50元的价格购进800件T恤.第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓,清仓时单价为40元.设第二个月单价降低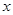 元.
元.
(1)填表:
| 时间 |
第一个月 |
第二个月 |
清仓 |
| 单价(元) |
80 |
|
40 |
| 销售量(件) |
200 |
|
|
(2)如果批发商希望通过销售这批T恤获利9 000元,那么第二个月的单价应是多少元?
丁丁推铅球的出手高度为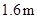 ,在如图所示的直角坐标系中,求铅球的落点与丁丁的距离.
,在如图所示的直角坐标系中,求铅球的落点与丁丁的距离.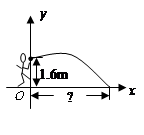
解方程: .
.
已知直线 及
及 外一点
外一点 ,分别按下列要求写出画法,并保留两图痕迹.
,分别按下列要求写出画法,并保留两图痕迹.
(1)在图1中,只用圆规在直线 上画出两点
上画出两点 ,使得点
,使得点 是一个等腰三角形的三个顶点;
是一个等腰三角形的三个顶点;
(2)在图2中,只用圆规在直线 外画出一点
外画出一点 ,使得点
,使得点 所在直线与直线
所在直线与直线 平行.
平行.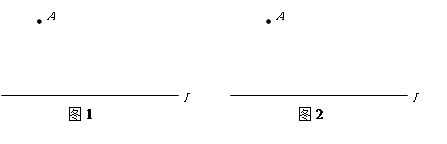
在平面内,先将一个多边形以点 为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为
为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为 ,并且原多边形上的任一点
,并且原多边形上的任一点 ,它的对应点
,它的对应点 在线段
在线段 或其延长线上;接着将所得多边形以点
或其延长线上;接着将所得多边形以点 为旋转中心,逆时针旋转一个角度
为旋转中心,逆时针旋转一个角度 ,这种经过和旋转的图形变换叫做旋转相似变换,记为
,这种经过和旋转的图形变换叫做旋转相似变换,记为 ,其中点
,其中点 叫做旋转相似中心,
叫做旋转相似中心, 叫做相似比,
叫做相似比, 叫做旋转角.
叫做旋转角.
(1)填空:
①如图1,将 以点
以点 为旋转相似中心,放大为原来的2倍,再逆时针旋转
为旋转相似中心,放大为原来的2倍,再逆时针旋转 ,得到
,得到 ,这个旋转相似变换记为
,这个旋转相似变换记为 (,);
(,);
②如图2, 是边长为
是边长为 的等边三角形,将它作旋转相似变换
的等边三角形,将它作旋转相似变换 ,得到
,得到 ,则线段
,则线段 的长为
的长为 ;
;
(2)如图3,分别以锐角三角形 的三边
的三边 ,
, ,
, 为边向外作正方形
为边向外作正方形 ,
, ,
, ,点
,点 ,
, ,
, 分别是这三个正方形的对角线交点,试分别利用
分别是这三个正方形的对角线交点,试分别利用 与
与 ,
, 与
与 之间的关系,运用旋转相似变换的知识说明线段
之间的关系,运用旋转相似变换的知识说明线段 与
与 之间的关系.
之间的关系.
在梯形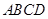 中,
中,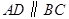 ,
,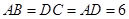 ,
,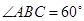 ,点
,点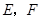 分别在线段
分别在线段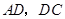 上(点
上(点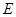 与点
与点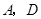 不重合),且
不重合),且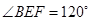 ,设
,设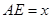 ,
,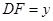 .
.
(1)求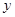 与
与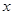 的函数表达式;
的函数表达式;
(2)当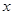 为何值时,
为何值时,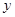 有最大值,最大值是多少?
有最大值,最大值是多少?