在平面内，先将一个多边形以点
为位似中心放大或缩小，使所得多边形与原多边形对应线段的比为
，并且原多边形上的任一点
，它的对应点
在线段
或其延长线上；接着将所得多边形以点为旋转中心，逆时针旋转一个角度
，这种经过和旋转的图形变换叫做旋转相似变换，记为
，其中点叫做旋转相似中心，叫做相似比，叫做旋转角．
（1）填空：
①如图1，将
以点
为旋转相似中心，放大为原来的2倍，再逆时针旋转
，得到
，这个旋转相似变换记为（ ， ）；
②如图2，是边长为
的等边三角形，将它作旋转相似变换
，得到，则线段
的长为 
；
（2）如图3，分别以锐角三角形
的三边
，
，
为边向外作正方形
，
，
，点
，
，
分别是这三个正方形的对角线交点，试分别利用
与
，
与
之间的关系，运用旋转相似变换的知识说明线段
与
之间的关系．
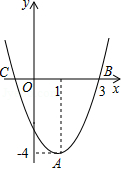
如图，在平面直角坐标系中，抛物线的顶点为 A（1，﹣4），且与 x轴交于 B、 C两点，点 B的坐标为（3，0）．
（1）写出 C点的坐标，并求出抛物线的解析式；
（2）观察图象直接写出函数值为正数时，自变量的取值范围．
已知二次函数 y＝ ax 2﹣2 ax+ c（ a＜0）的最大值为4，且抛物线过点（ ，﹣ ，点 P（ t，0）是 x轴上的动点，抛物线与 y轴交点为 C，顶点为 D．
（1）求该二次函数的解析式，及顶点 D的坐标；
（2）求| PC﹣ PD|的最大值及对应的点 P的坐标；
（3）设 Q（0，2 t）是 y轴上的动点，若线段 PQ与函数 y＝ a| x| 2﹣2 a| x|+ c的图象只有一个公共点，求 t的取值．
如图，已知 AD是△ ABC的外角∠ EAC的平分线，交 BC的延长线于点 D，延长 DA交△ ABC的外接圆于点 F，连接 FB， FC．
（1）求证：∠ FBC＝∠ FCB；
（2）已知 FA• FD＝12，若 AB是△ ABC外接圆的直径， FA＝2，求 CD的长．
已知反比例函数 y＝ 的图象在二四象限，一次函数为 y＝ kx+ b（ b＞0），直线 x＝1与 x轴交于点 B，与直线 y＝ kx+ b交于点 A，直线 x＝3与 x轴交于点 C，与直线 y＝ kx+ b交于点 D．
（1）若点 A， D都在第一象限，求证： b＞﹣3 k；
（2）在（1）的条件下，设直线 y＝ kx+ b与 x轴交于点 E与 y轴交于点 F，当 ＝ 且△ OFE的面积等于 时，求这个一次函数的解析式，并直接写出不等式 ＞ kx+ b的解集．
某一公路的道路维修工程，准备从甲、乙两个工程队选一个队单独完成．根据两队每天的工程费用和每天完成的工程量可知，若由两队合做此项维修工程，6天可以完成，共需工程费用385200元，若单独完成此项维修工程，甲队比乙队少用5天，每天的工程费用甲队比乙队多4000元，从节省资金的角度考虑，应该选择哪个工程队？