已知二次函数 y＝ ax 2﹣2 ax+ c（ a＜0）的最大值为4，且抛物线过点（ ，﹣ ，点 P（ t，0）是 x轴上的动点，抛物线与 y轴交点为 C，顶点为 D．
（1）求该二次函数的解析式，及顶点 D的坐标；
（2）求| PC﹣ PD|的最大值及对应的点 P的坐标；
（3）设 Q（0，2 t）是 y轴上的动点，若线段 PQ与函数 y＝ a| x| 2﹣2 a| x|+ c的图象只有一个公共点，求 t的取值．
计算：
解不等式组：
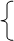
，并把解集在数轴上表示出来
如图，已知抛物线
与
轴交于A、B两点，与
轴交于点C．求A、B、C三点的坐标．
过点A作AP∥CB交抛物线于点P，求四边形ACBP的面积．
在
轴上方的抛物线上是否存在一点M，过M作MG
轴于点G，使以A、M、G三点为顶点的三角形与
PCA相似．若存在，直接写出所有满足要求的M点的坐标；否则，请说明理由．
如图，在Rt△ABC中，∠A＝90°，AB＝6，AC＝8，D、E分别是边AB、AC的中点，点P从点D出发沿DE方向运动，过点P作PQ⊥BC于Q，过点Q作QR‖BA交AC于R，当点Q与点C重合时，点P停止运动．求点D到BC的距离DH的长；
设BQ＝x, QR＝y．
① 求y关于x的函数关系式（0≤x≤10）；
② 是否存在点P，使△PQR为等腰三角形？若存在，求出所有满足要求的x的值；若不存在，请说明理由．
为缓解油价上涨给出租车行业带来的成本压力，某巿自2012年5月1日起，调
为缓解油价上涨给出租车行业带来的成本压力，某巿自2012年5月1日起，调整出租车运价，调整方案见下列表格及图像（其中a,b为常数）.
| 行驶路程 |
收费标准 |
|
| 调价前 |
调价后 |
|
| 不超过3km的部分 |
起步价6元 |
起步价a元 |
| 超过3km的部分 |
每公里2.1元 |
每公里b元 |
设行驶路程x km时，调价前的运价为y1（元），调价后的运价为y2（元）.如图，折线ABC表示y2与x之间的函数关系式，线段EF表示当0≤x≤3时，y1与x的函数关系式，根据图表信息，完成下列各题： 填空：a=, b=.
写出当x＞3时，y1与x的函数关系式，并在上图中画出该函数的图象.
函数y1与y2的图象是否存在交点？若存在，求出交点的坐标，并说明该点的实际意义；若不存在，请说明理由.
已知，如图，AB为⊙O的直径，弦DC延长线上有一点P，∠PAC＝∠PDA.求证：PA是⊙O的切线；
若AD＝6，∠ACD＝60°, 求⊙O的半径.
